Page 200 - Schaum's Outline of Theory and Problems of Electric Circuits

HIGHER-ORDER CIRCUITS AND COMPLEX FREQUENCY
CHAP. 8]

Fig. 8-43 189
4
8.47 In the circuit of Fig. 8-44 let R 1 ¼ 9 k
¼ 9R 2 , C 2 ¼ 100 pF ¼ 9C 1 , and v 1 ¼ 10 t V. Find i at 1 ms after
the switch is closed. Ans: i ¼ 1:0001 mA

Fig. 8-44

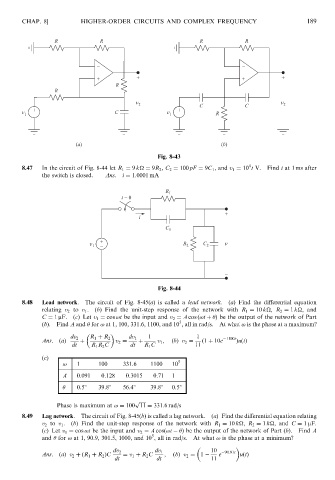
8.48 Lead network. The circuit of Fig. 8-45(a) is called a lead network. (a) Find the differential equation
relating v 2 to v 1 . (b) Find the unit-step response of the network with R 1 ¼ 10 k
, R 2 ¼ 1 k
, and
C ¼ 1 mF. (c) Let v 1 ¼ cos !t be the input and v 2 ¼ A cos ð!t þ Þ be the output of the network of Part
5
(b). Find A and for ! at 1, 100, 331.6, 1100, and 10 , all in rad/s. At what ! is the phase at a maximum?

dv 2 R 1 þ R 2 dv 1 1 1 1100t
Ans: ðaÞ þ v 2 ¼ þ v 1 ; ðbÞ v 2 ¼ ð1 þ 10e ÞuðtÞ
dt R 1 R 2 C dt R 1 C 11
(c)
! 1 100 331.6 1100 10 5
A 0.091 0.128 0.3015 0.71 1

0.58 39:88 56.48 39.88 0.58
p ffiffiffiffiffi
Phase is maximum at ! ¼ 100 11 ¼ 331:6 rad/s
8.49 Lag network. The circuit of Fig. 8-45(b) is called a lag network. (a) Find the differential equation relating
v 2 to v 1 . (b) Find the unit-step response of the network with R 1 ¼ 10 k
, R 2 ¼ 1 k
, and C ¼ 1 mF.
(c) Let v 1 ¼ cos !t be the input and v 2 ¼ A cosð!t Þ be the output of the network of Part (b). Find A
5
and for ! at 1, 90.9, 301.5, 1000, and 10 , all in rad/s. At what ! is the phase at a minimum?

dv 2 dv 1 10 90:91t
Ans: ðaÞ v 2 þðR 1 þ R 2 ÞC ¼ v 1 þ R 2 C ; ðbÞ v 2 ¼ 1 e uðtÞ
dt dt 11