Page 195 - Schaum's Outline of Theory and Problems of Electric Circuits

HIGHER-ORDER CIRCUITS AND COMPLEX FREQUENCY
[CHAP. 8
184
The voltage transfer function remains unchanged by magnitude scaling. In general, any dimensionless
transfer function is unaffected by magnitude scaling; a transfer function having units
is multiplied by K m ;
and a function having units S is multiplied by 1=K m .

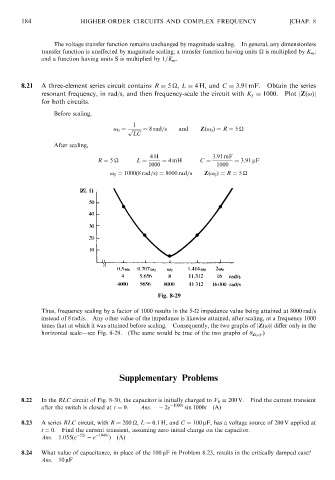
8.21 A three-element series circuit contains R ¼ 5
, L ¼ 4 H, and C ¼ 3:91 mF. Obtain the series
resonant frequency, in rad/s, and then frequency-scale the circuit with K f ¼ 1000. Plot jZð!Þj
for both circuits.
Before scaling,
1
! 0 ¼ p ffiffiffiffiffiffiffi ¼ 8 rad=s and Zð! 0 Þ¼ R ¼ 5
LC
After scaling,
4H 3:91 mF
R ¼ 5
L ¼ ¼ 4mH C ¼ ¼ 3:91 mF
1000 1000
! 0 ¼ 1000ð8 rad=sÞ¼ 8000 rad=s Zð! 0 Þ¼ R ¼ 5

Fig. 8-29

Thus, frequency scaling by a factor of 1000 results in the 5-
impedance value being attained at 8000 rad/s
instead of 8 rad/s. Any other value of the impedance is likewise attained, after scaling, at a frequency 1000
times that at which it was attained before scaling. Consequently, the two graphs of jZð!Þj differ only in the
horizontal scale—see Fig. 8-29. (The same would be true of the two graphs of Zð!Þ .)

Supplementary Problems

8.22 In the RLC circuit of Fig. 8-30, the capacitor is initially charged to V 0 ¼ 200 V. Find the current transient
after the switch is closed at t ¼ 0. Ans: 2e 1000t sin 1000t ðAÞ

8.23 A series RLC circuit, with R ¼ 200
, L ¼ 0:1 H, and C ¼ 100 mF, has a voltage source of 200 V applied at
t ¼ 0. Find the current transient, assuming zero initial charge on the capacitor.
52t 1948t
Ans: 1:055ðe e Þ ðAÞ
8.24 What value of capacitance, in place of the 100 mF in Problem 8.23, results in the critically damped case?
Ans: 10 mF