Page 194 - Schaum's Outline of Theory and Problems of Electric Circuits

183
HIGHER-ORDER CIRCUITS AND COMPLEX FREQUENCY
CHAP. 8]
The denominator is the same as that in Problem 8.17, with the same roots and corresponding natural
frequencies.

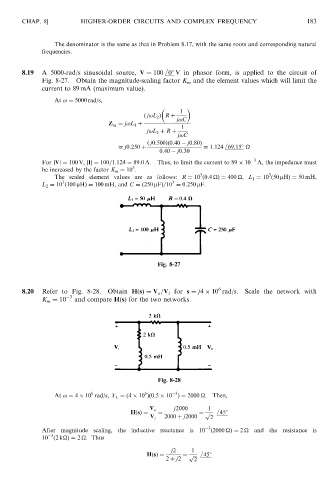
8.19 A 5000-rad/s sinusoidal source, V ¼ 100 08 V in phasor form, is applied to the circuit of
Fig. 8-27. Obtain the magnitude-scaling factor K m and the element values which will limit the
current to 89 mA (maximum value).
At ! ¼ 5000 rad/s,

1
ð j!L 2 Þ R þ
j!C
Z in ¼ j!L 1 þ
1
j!L 2 þ R þ
j!C
ð j0:500Þð0:40 j0:80Þ
¼ j0:250 þ ¼ 1:124 69:158
0:40 j0:30
3
For jVj¼ 100 V, jIj¼ 100=1:124 ¼ 89:0 A. Thus, to limit the current to 89 10 A, the impedance must
3
be increased by the factor K m ¼ 10 .
3 3
The scaled element values are as follows: R ¼ 10 ð0:4
Þ¼ 400
, L 1 ¼ 10 ð50 mHÞ¼ 50 mH,
3 3
L 2 ¼ 10 ð100 mHÞ¼ 100 mH, and C ¼ð250 mFÞ=10 ¼ 0:250 mF.

Fig. 8-27

6
8.20 Refer to Fig. 8-28. Obtain HðsÞ¼ V =V for s ¼ j4 10 rad/s. Scale the network with
o
i
K ¼ 10 3 and compare HðsÞ for the two networks.
m

Fig. 8-28

3
6
6
At ! ¼ 4 10 rad/s, X L ¼ð4 10 Þð0:5 10 Þ¼ 2000
. Then,
j2000 1
V o
HðsÞ¼ ¼ ¼ p ffiffiffi 458
V i 2000 þ j2000 2
3
After magnitude scaling, the inductive reactance is 10 ð2000
Þ¼ 2
and the resistance is
3
10 ð2k
Þ¼ 2
. Thus
j2 1
HðsÞ¼ ¼ p ffiffiffi 458
2 þ j2 2