Page 96 - Schaum's Outline of Theory and Problems of Electric Circuits

85
AMPLIFIERS AND OPERATIONAL AMPLIFIER CIRCUITS
CHAP. 5]
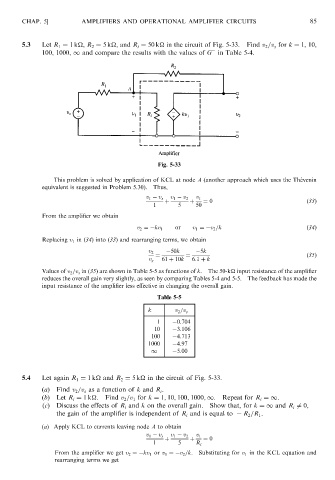
5.3 Let R 1 ¼ 1k
, R 2 ¼ 5k
,and R i ¼ 50 k
in the circuit of Fig. 5-33. Find v 2 =v s for k ¼ 1, 10,

100, 1000, 1 and compare the results with the values of G in Table 5-4.

Fig. 5-33

This problem is solved by application of KCL at node A (another approach which uses the The ´ venin
equivalent is suggested in Problem 5.30). Thus,
v 1 v s v 1 v 2 v 1
þ þ ¼ 0 ð33Þ
1 5 50
From the amplifier we obtain
or v 1 ¼ v 2 =k ð34Þ
v 2 ¼ kv 1
Replacing v 1 in (34) into (33) and rearranging terms, we obtain
50k 5k
v 2
¼ ¼ ð35Þ
v s 61 þ 10k 6:1 þ k
Values of v 2 =v s in (35) are shown in Table 5-5 as functions of k. The 50-k
input resistance of the amplifier
reduces the overall gain very slightly, as seen by comparing Tables 5-4 and 5-5. The feedback has made the
input resistance of the amplifier less effective in changing the overall gain.

Table 5-5
k v 2 =v s
1 0:704
10 3:106
100 4:713
1000 4:97
1 5:00

5.4 Let again R 1 ¼ 1k
and R 2 ¼ 5k
in the circuit of Fig. 5-33.
ðaÞ Find v 2 =v s as a function of k and R i :
ðbÞ Let R i ¼ 1k
.Find v 2 =v 1 for k ¼ 1; 10; 100; 1000; 1. Repeat for R i ¼1:
ðcÞ Discuss the effects of R i and k on the overall gain. Show that, for k ¼1 and R i 6¼ 0;
the gain of the amplifier is independent of R i and is equal to R 2 =R 1 :

(a) Apply KCL to currents leaving node A to obtain
v 1 v s v 1 v 2 v 1
þ þ ¼ 0
1 5 R i
From the amplifier we get v 2 ¼ kv 1 or v 1 ¼ v 2 =k. Substituting for v 1 in the KCL equation and
rearranging terms we get