Page 107 - Schaum's Outline of Theory and Problems of Signals and Systems

96 LINEAR TIME-INVARIANT SYSTEMS [CHAP. 2

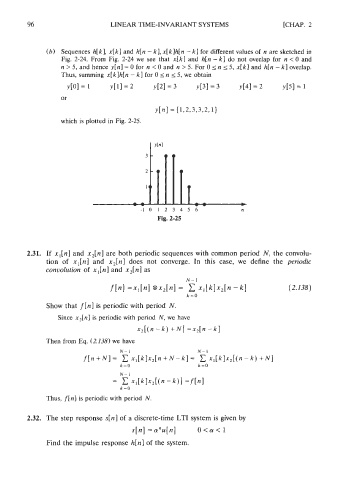
(b) Sequences h[k], x[kl and h[n - k], x[k]h[n - kl for different values of n are sketched in
Fig. 2-24. From Fig. 2-24 we see that x[k J and h[n - k] do not overlap for n < 0 and
n > 5, and hence y[n] = 0 for n < 0 and n > 5. For 0 5 n 1: 5, x[k] and h[n - k] overlap.
Thus, summing x[k]h[n - k] for 0 sn 2 5, we obtain

which is plotted in Fig. 2-25.

Fig. 2-25

2.31. If x,[n] and x2[n] are both periodic sequences with common period N, the convolu-
tion of x,[n] and x2[n] does not converge. In this case, we define the periodic
convolution of x,[n] and x2[n] as

Show that f [n] is periodic with period N.
Since x,[n] is periodic with period N, we have

Then from Eq. (2.138) we have

Thus, f [n 1 is periodic with period N.

2.32. The step response s[n] of a discrete-time LTI system is given by
s[n] = anu[n] O<a<l

Find the impulse response h[n] of the system.