Page 108 - Schaum's Outline of Theory and Problems of Signals and Systems

CHAP. 21 LINEAR TIME-INVARIANT SYSTEMS

From Eq. (2.41) the impulse response h[nl is given by
h[n] = s[n] - s[n - 11 = crnu[n] - a"-'u[n - 11
= {S[n] +anu[n - 11) -an-'u[n - 11

= 6[n] - (1 - a)crn-'u[n - 11

PROPERTIES OF DISCRETE-TIME LTI SYSTEMS

2.33. Show that if the input x[n] to a discrete-time LTI system is periodic with period N,
then the output y[n] is also periodic with period N.
Let h[n] be the impulse response of the system. Then by Eq. (2.39) we have

Let n=m+N.Then
m 10
y[m + N] = h[k]x[m + N - k] = C h[k]x[(m - k) + N]
k= -m k= -03
Since x[n] is periodic with period N, we have
x[(m-k) +N] =x[m-k]
OD
Thus, y[m + N] = h[k]x[m - k] = y[m]
k- -OD
which indicates that the output y[n] is periodic with period N.

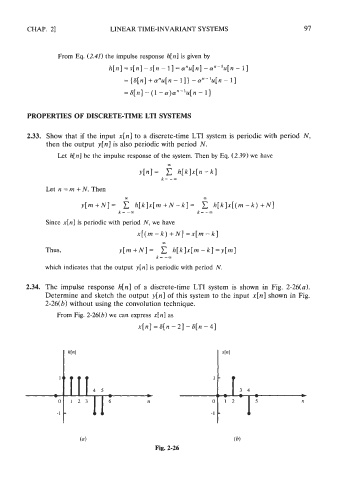
2.34. The impulse response h[n] of a discrete-time LTI system is shown in Fig. 2-26(a).
Determine and sketch the output y[n] of this system to the input x[n] shown in Fig.
2-26(b) without using the convolution technique.
From Fig. 2-26(b) we can express x[n] as
x[n] = 6[n - 21 - S[n - 41

(b)
Fig. 2-26