Page 47 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

The Crystal Lattice System

b
a
b
c c
a

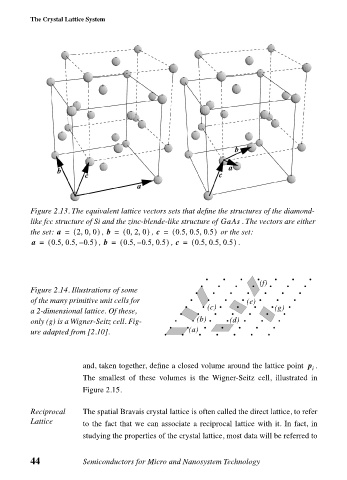
Figure 2.13. The equivalent lattice vectors sets that define the structures of the diamond-
like fcc structure of Si and the zinc-blende-like structure of GaAs . The vectors are either
,
,
,,
,,
the set: a = ( 200) , b = ( 020) , c = ( 0.5 0.5 0.5) or the set:
,
,
,
,
,
,
a = ( 0.5 0.5 – 0.5) , b = ( 0.5 – 0.5 0.5) , c = ( 0.5 0.5 0.5) .
(f)
Figure 2.14. Illustrations of some
of the many primitive unit cells for (e)
(c) (g)
a 2-dimensional lattice. Of these,
only (g) is a Wigner-Seitz cell. Fig- (b) (d)
ure adapted from [2.10]. (a)

and, taken together, define a closed volume around the lattice point p .
i
The smallest of these volumes is the Wigner-Seitz cell, illustrated in
Figure 2.15.

Reciprocal The spatial Bravais crystal lattice is often called the direct lattice, to refer
Lattice to the fact that we can associate a reciprocal lattice with it. In fact, in
studying the properties of the crystal lattice, most data will be referred to

44 Semiconductors for Micro and Nanosystem Technology