Page 50 - Semiconductor For Micro- and Nanotechnology An Introduction For Engineers

Crystal Structure
Box 2.1. Plane waves and wave-vectors.
We describe a general plane wave with counts the number cycles completed along a spa-
(
i kr ωt) tial segment.
⋅
–
(
,
ψ r t) = Ae . (B 2.1.1)
If we fix the time t (“freezing” the wave in space
Recalling the relation between the trigonometric
and time), then moving along a spatial direction
functions and the exponential function,
we will experience a wave-like variation of the
iθ
e = cos θ () + i sin θ () . (B 2.1.2) amplitude of ψ as kr⋅ . If we now move in a
we see that ψ is indeed a wave-like function, for direction perpendicular to the propagation of the
θ parametrizes an endless circular cycle on the wave , then we will experience no amplitude
k
complex plane. modulation. Next, staying in the perpendicular
direction to the wave propagation at a fixed posi-
I iθ
e tion, if the time is again allowed to vary, we will
now experience an amplitude modulation as the
wave moves past us.
θ
R
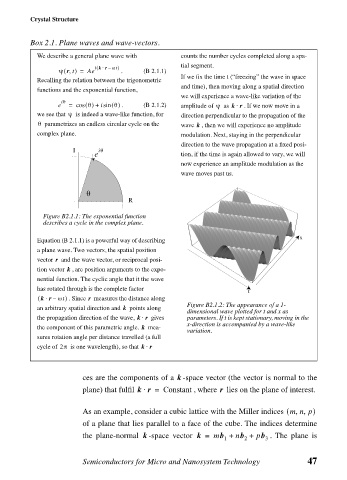
Figure B2.1.1: The exponential function
describes a cycle in the complex plane.
x
Equation (B 2.1.1) is a powerful way of describing
a plane wave. Two vectors, the spatial position
vector and the wave vector, or reciprocal posi-
r
tion vector , are position arguments to the expo-
k
nential function. The cyclic angle that it the wave
has rotated through is the complete factor
t
⋅
( kr ωt) . Since measures the distance along
–
r
Figure B2.1.2: The appearance of a 1-
k
an arbitrary spatial direction and points along
dimensional wave plotted for t and x as
the propagation direction of the wave, kr⋅ gives parameters. If t is kept stationary, moving in the
x-direction is accompanied by a wave-like
the component of this parametric angle. mea-
k
variation.
sures rotation angle per distance travelled (a full
cycle of 2π is one wavelength), so that kr⋅
ces are the components of a -space vector (the vector is normal to the
k
plane) that fulfil kr⋅ = Constant , where lies on the plane of interest.
r
As an example, consider a cubic lattice with the Miller indices mn p,,( )
of a plane that lies parallel to a face of the cube. The indices determine
k
the plane-normal -space vector k = mb + nb + pb . The plane is
1 2 3
Semiconductors for Micro and Nanosystem Technology 47