Page 186 - Shigley's Mechanical Engineering Design

bud29281_ch04_147-211.qxd 11/27/09 2:55PM Page 161 ntt 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

Deflection and Stiffness 161
2
6
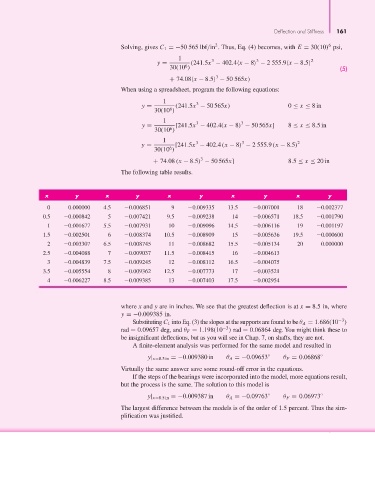
Solving, gives C 1 =−50 565 lbf/in . Thus, Eq. (4) becomes, with E = 30(10) psi,
1 3 3 2
y = (241.5x − 402.4 x − 8 − 2 555.9 x − 8.5
6
30(10 ) (5)
3
+ 74.08 x − 8.5 − 50 565x)
When using a spreadsheet, program the following equations:
1 3
y = (241.5x − 50 565x) 0 ≤ x ≤ 8in
6
30(10 )
1 3 3
y = [241.5x − 402.4(x − 8) − 50 565x] 8 ≤ x ≤ 8.5in
6
30(10 )
1 3 3 2
y = [241.5x − 402.4 (x − 8) − 2 555.9 (x − 8.5)
6
30(10 )
3
+ 74.08 (x − 8.5) − 50 565x] 8.5 ≤ x ≤ 20 in
The following table results.

x y x y x y x y x y
0 0.000000 4.5 0.006851 9 0.009335 13.5 0.007001 18 0.002377
0.5 0.000842 5 0.007421 9.5 0.009238 14 0.006571 18.5 0.001790
1 0.001677 5.5 0.007931 10 0.009096 14.5 0.006116 19 0.001197
1.5 0.002501 6 0.008374 10.5 0.008909 15 0.005636 19.5 0.000600
2 0.003307 6.5 0.008745 11 0.008682 15.5 0.005134 20 0.000000
2.5 0.004088 7 0.009037 11.5 0.008415 16 0.004613
3 0.004839 7.5 0.009245 12 0.008112 16.5 0.004075
3.5 0.005554 8 0.009362 12.5 0.007773 17 0.003521
4 0.006227 8.5 0.009385 13 0.007403 17.5 0.002954

where x and y are in inches. We see that the greatest deflection is at x = 8.5 in, where
y =−0.009385 in.
−3
Substituting C 1 into Eq. (3) the slopes at the supports are found to be θ A = 1.686(10 )
−3
rad = 0.09657 deg, and θ F = 1.198(10 ) rad = 0.06864 deg. You might think these to
be insignificant deflections, but as you will see in Chap. 7, on shafts, they are not.
A finite-element analysis was performed for the same model and resulted in
y| x=8.5in =−0.009380 in θ A =−0.09653 ◦ θ F = 0.06868 ◦
Virtually the same answer save some round-off error in the equations.
If the steps of the bearings were incorporated into the model, more equations result,
but the process is the same. The solution to this model is

y| x=8.5in =−0.009387 in θ A =−0.09763 ◦ θ F = 0.06973 ◦
The largest difference between the models is of the order of 1.5 percent. Thus the sim-
plification was justified.