Page 551 - Shigley's Mechanical Engineering Design

bud29281_ch10_517-568.qxd 12/16/2009 7:14 pm Page 525 pinnacle 203:MHDQ196:bud29281:0073529281:bud29281_pagefiles:

Mechanical Springs 525
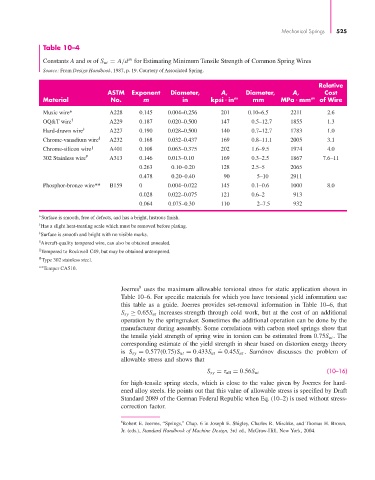
Table 10–4

Constants A and m of S ut = A/d for Estimating Minimum Tensile Strength of Common Spring Wires
m
Source: From Design Handbook, 1987, p. 19. Courtesy of Associated Spring.

Relative
ASTM Exponent Diameter, A, Diameter, A, Cost
Material No. m in kpsi in m mm MPa mm m of Wire

Music wire* A228 0.145 0.004–0.256 201 0.10–6.5 2211 2.6
OQ&T wire † A229 0.187 0.020–0.500 147 0.5–12.7 1855 1.3
Hard-drawn wire ‡ A227 0.190 0.028–0.500 140 0.7–12.7 1783 1.0
Chrome-vanadium wire § A232 0.168 0.032–0.437 169 0.8–11.1 2005 3.1
Chrome-silicon wire A401 0.108 0.063–0.375 202 1.6–9.5 1974 4.0
302 Stainless wire # A313 0.146 0.013–0.10 169 0.3–2.5 1867 7.6–11
0.263 0.10–0.20 128 2.5–5 2065
0.478 0.20–0.40 90 5–10 2911
Phosphor-bronze wire** B159 0 0.004–0.022 145 0.1–0.6 1000 8.0
0.028 0.022–0.075 121 0.6–2 913
0.064 0.075–0.30 110 2–7.5 932

Surface is smooth, free of defects, and has a bright, lustrous finish.
∗
† Has a slight heat-treating scale which must be removed before plating.
‡ Surface is smooth and bright with no visible marks.
§ Aircraft-quality tempered wire, can also be obtained annealed.
Tempered to Rockwell C49, but may be obtained untempered.

# Type 302 stainless steel.
Temper CA510.
∗∗

8
Joerres uses the maximum allowable torsional stress for static application shown in
Table 10–6. For specific materials for which you have torsional yield information use
this table as a guide. Joerres provides set-removal information in Table 10–6, that
S sy ≥ 0.65S ut increases strength through cold work, but at the cost of an additional
operation by the springmaker. Sometimes the additional operation can be done by the
manufacturer during assembly. Some correlations with carbon steel springs show that
the tensile yield strength of spring wire in torsion can be estimated from 0.75S ut . The
corresponding estimate of the yield strength in shear based on distortion energy theory
.
is S sy = 0.577(0.75)S ut = 0.433S ut = 0.45S ut . Samónov discusses the problem of
allowable stress and shows that
(10–16)
S sy = τ all = 0.56S ut
for high-tensile spring steels, which is close to the value given by Joerres for hard-
ened alloy steels. He points out that this value of allowable stress is specified by Draft
Standard 2089 of the German Federal Republic when Eq. (10–2) is used without stress-
correction factor.

8 Robert E. Joerres, “Springs,” Chap. 6 in Joseph E. Shigley, Charles R. Mischke, and Thomas H. Brown,
Jr. (eds.), Standard Handbook of Machine Design, 3rd ed., McGraw-Hill, New York, 2004.