Page 224 - Soil and water contamination, 2nd edition

Substance transport 211
2.0
6955
1.5
erfc(β) 1.0

0.5

0
-3 -2 -1 0 1 2 3
β
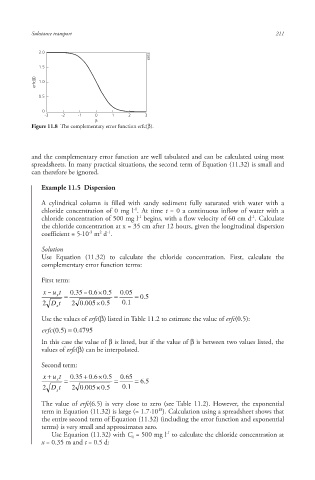
Figure 11.8 The complementary error function erfc(β).

and the complementary error function are well tabulated and can be calculated using most
spreadsheets. In many practical situations, the second term of Equation (11.32) is small and
can therefore be ignored.

Example 11.5 Dispersion

A cylindrical column is filled with sandy sediment fully saturated with water with a
-1
chloride concentration of 0 mg l . At time t = 0 a continuous inflow of water with a
-1
-1
chloride concentration of 500 mg l begins, with a flow velocity of 60 cm d . Calculate
the chloride concentration at x = 35 cm after 12 hours, given the longitudinal dispersion
-3
2
-1
coefficient = 5·10 m d .
Solution
Use Equation (11.32) to calculate the chloride concentration. First, calculate the
complementary error function terms:
First term:
x u x t . 0 35 6 . 0 5 . 0 . 0 05
5 . 0
2 D t 2 . 0 005 5 . 0 1 . 0
x
Use the values of erfc(β) listed in Table 11.2 to estimate the value of erfc(0.5):
erfc ) 5 . 0 ( . 0 4795

In this case the value of β is listed, but if the value of β is between two values listed, the
values of erfc(β) can be interpolated.

Second term:
x u t . 0 35 6 . 0 5 . 0 . 0 65
x
5 . 6
2 D t 2 . 0 005 5 . 0 1 . 0
x
The value of erfc(6.5) is very close to zero (see Table 11.2). However, the exponential
18
term in Equation (11.32) is large (≈ 1.7·10 ). Calculation using a spreadsheet shows that
the entire second term of Equation (11.32) (including the error function and exponential
terms) is very small and approximates zero.
-1
Use Equation (11.32) with C = 500 mg l to calculate the chloride concentration at
0
x = 0.35 m and t = 0.5 d:

10/1/2013 6:44:57 PM
Soil and Water.indd 223 10/1/2013 6:44:57 PM
Soil and Water.indd 223