Page 48 - Standard Handbook Of Petroleum & Natural Gas Engineering

Differential and Integral Calculus 37

Higher-Order Derivatives

The second derivative of a function y = f(x), denoted f"(x) or dzy/dx2 is the
derivative of f'(x) and the third derivative, f"'(x) is the derivative of f"(x).
Geometrically, in terms of f(x): if f"(x) 0 then f(x) is concave upwardly, if f"(x)
< 0 then f(x) is concave downwardly.

Partial Derivatives
If u = f(x,y, . . .) is a function of two or more variables, the partial derivative
of u with respect to x, fx(x,y, . . .) or &/ax, may be formed by assuming x to
be the independent variable and holding (y, . . .) as constants. In a similar
manner, fy(x,y, . . .) or au/ay may be formed by holding (x, . . .) as constants.
Second-order partial derivatives of f(x,y) are denoted by the manner of their
formation as fm, f, (equal to f,,), f, or as a2u/ax2, a2u/axay, a2u/ay2, and the
higher-order partia! derivatives are likewise formed.
Implicit functions, i.e., f(x,y) = 0, may be solved by the formula

at the point in question.

Maxima and Minima
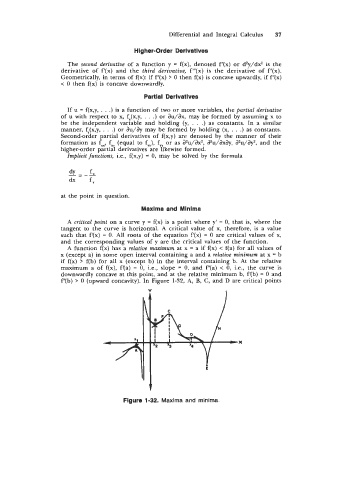
A critical point on a curve y = f(x) is a point where y' = 0, that is, where the
tangent to the curve is horizontal. A critical value of x, therefore, is a value
such that f'(x) = 0. All roots of the equation f'(x) = 0 are critical values of x,
and the corresponding values of y are the critical values of the function.
A function f(x) has a relative maximum at x = a if f(x) < f(a) for all values of
x (except a) in some open interval containing a and a relative minimum at x = b
if f(x) > f(b) for all x (except b) in the interval containing b. At the relative
maximum a of f(x), f'(a) = 0, i.e., slope = 0, and f"(a) < 0, Le., the curve is
downwardly concave at this point, and at the relative minimum b, f'(b) = 0 and
f"(b) > 0 (upward concavity). In Figure 1-32, A, B, C, and D are critical points

Figure 1-32. Maxima and minima.