Page 45 - Standard Handbook Of Petroleum & Natural Gas Engineering

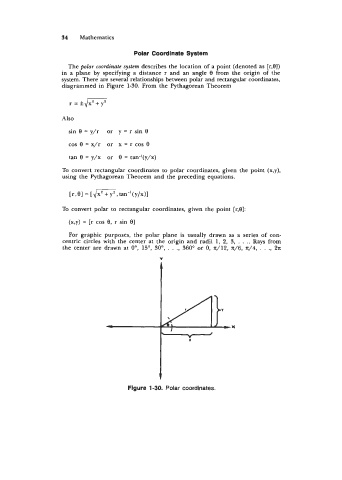
34 Mathematics

Polar Coordinate System
The polar coordinate system describes the location of a point (denoted as [r,81)
in a plane by specifying a distance r and an angle 8 from the origin of the
system. There are several relationships between polar and rectangular coordinates,
diagrammed in Figure 1-30. From the Pythagorean Theorem

Also
sin 8 = y/r or y = r sin 8

cos 8 = x/r or x = r cos 8
tan 8 = y/x or 8 = tan-'(y/x)

To convert rectangular coordinates to polar coordinates, given the point (x,y),
using the Pythagorean Theorem and the preceding equations.

= [J-,tan-'(y/x)]
[r,~]
To convert polar to rectangular coordinates, given the point [r,eI:

(x,y) = [r cos 8, r sin 81
For graphic purposes, the polar plane is usually drawn as a series of con-
centric circles with the center at the origin and radii 1, 2, 3, . . .. Rays from
the center are drawn at 0", 15", 30°, . . ., 360' or 0, 7t/12, x/6, n/4, . . ., 27t
V

Figure 1-30. Polar coordinates.