Page 319 - Standard Handbook Petroleum Natural Gas Engineering VOLUME2

286 Reservoir Engineering

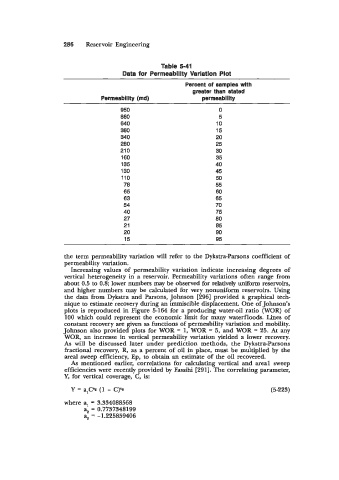
Table 5-41
Data for Permeabilitv Variation Plot
Percent of samples with
greater than stated
Permeability (md) Permeability
950 0
860 5
640 10
380 15
340 20
280 25
21 0 30
160 35
135 40
130 45
110 50
78 55
65 60
63 65
54 70
40 75
27 80
21 85
20 90
15 95

the term permeability variation will refer to the Dykstra-Parsons coefficient of
permeability variation.
Increasing values of permeability variation indicate increasing degrees of
vertical heterogeneity in a reservoir. Permeability variations often range from
about 0.5 to 0.8; lower numbers may be observed for relatively uniform reservoirs,
and higher numbers may be calculated for very nonuniform reservoirs. Using
the data from Dykstra and Parsons, Johnson [296] provided a graphical tech-
nique to estimate recovery during an immiscible displacement. One of Johnson’s
plots is reproduced in Figure 5-164 for a producing water-oil ratio (WOR) of
100 which could represent the economic limit for many waterfloods. Lines of
constant recovery are given as functions of permeability variation and mobility.
Johnson also provided plots for WOR = 1, WOR = 5, and WOR = 25. At any
WOR, an increase in vertical permeability variation yielded a lower recovery.
As will be discussed later under prediction methods, the Dykstra-Parsons
fractional recovery, R, as a percent of oil in place, must be multiplied by the
areal sweep efficiency, Ep, to obtain an estimate of the oil recovered.
As mentioned earlier, correlations for calculating vertical and areal sweep
efficiencies were recently provided by Fassihi [291]. The correlating parameter,
Y, for vertical coverage, C, is:

Y = a,Ct (1 - C)% (5-223)
where a, = 3.334088568
= 0.7737348199
-1.225859406