Page 152 - Statistics and Data Analysis in Geology

Analysis of Multivariate Data

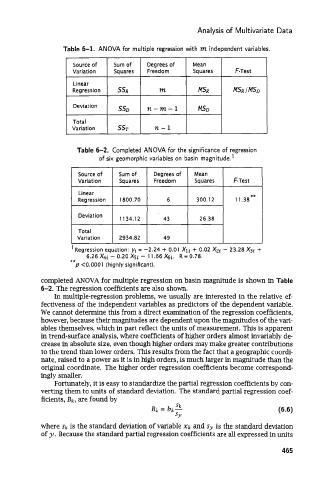
Table 6-1. ANOVA for multiple regression with m independent variables.

Variation Squares F-Test
Linear
MSR I MSD

t I I I I I

Table 6-2. Completed ANOVA for the significance of regression
of six geomorphic variables on basin magnitude.'

Source of Sum of Degrees of Mean
Variation Squares Freedom Squares F-Test

Linear
Regression 1800.70 6 300.12 11.38**

Deviation
34. 43 26.38
Total
Variation 2934.82 49

completed ANOVA for multiple regression on basin magnitude is shown in Table
6-2. The regression coefficients are also shown.
In multiple-regression problems, we usually are interested in the relative ef-
fectiveness of the independent variables as predictors of the dependent variable.
We cannot determine this from a direct examination of the regression coefficients,
however, because their magnitudes are dependent upon the magnitudes of the vari-
ables themselves, which in part reflect the units of measurement. This is apparent
in trend-surface analysis, where coefficients of higher orders almost invariably de-
crease in absolute size, even though higher orders may make greater contributions
to the trend than lower orders. This results from the fact that a geographic coordi-
nate, raised to a power as it is in high orders, is much larger in magnitude than the
original coordinate. The higher order regression coefficients become correspond-
ingly smaller.
Fortunately, it is easy to standardize the partial regression coefficients by con-
verting them to units of standard deviation. The standard partial regression coef-
ficients, &, are found by
sk
Bk = bk- (6.6)
SY
where Sk is the standard deviation of variable xk and sy is the standard deviation
of y. Because the standard partial regression coefficients are all expressed in units

465