Page 155 - Statistics and Data Analysis in Geology

Statistics and Data Analysis in Geology- Chapter 6

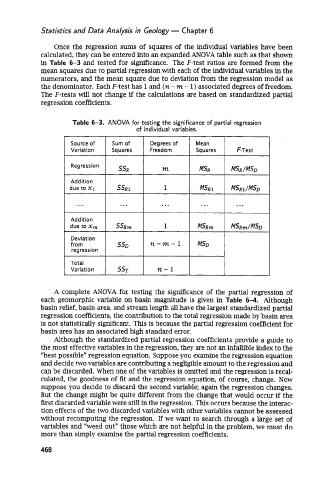
Once the regression sums of squares of the individual variables have been
calculated, they can be entered into an expanded ANOVA table such as that shown
in Table 6-3 and tested for significance. The F-test ratios are formed from the
mean squares due to partial regression with each of the individual variables in the
numerators, and the mean square due to deviation from the regression model as
the denominator. Each F-test has 1 and (n - m - 1) associated degrees of freedom.
The F-tests will not change if the calculations are based on standardized partial
regression coefficients.

Table 6-3. ANOVA for testing the significance of partial regression
of individual variables.

A complete ANOVA for testing the significance of the partial regression of
each geomorphic variable on basin magnitude is given in Table 6-4. Although
basin relief, basin area, and stream length all have the largest standardized partial
regression coefficients, the contribution to the total regression made by basin area
is not statistically significant. This is because the partial regression coefficient for
basin area has an associated high standard error.
Although the standardized partial regression coefficients provide a guide to
the most effective variables in the regression, they are not an infallible index to the
“best possible’’ regression equation. Suppose you examine the regression equation
and decide two variables are contributing a negligible amount to the regression and
can be discarded. When one of the variables is omitted and the regression is recal-
culated, the goodness of fit and the regression equation, of course, change. Now
suppose you decide to discard the second variable; again the regression changes.
But the change might be quite different from the change that would occur if the
first discarded variable were still in the regression. This occurs because the interac-
tion effects of the two discarded variables with other variables cannot be assessed
without recomputing the regression. If we want to search through a large set of
variables and “weed out” those which are not helpful in the problem, we must do
more than simply examine the partial regression coefficients.

468