Page 28 - Statistics and Data Analysis in Geology

Elementary Statistics

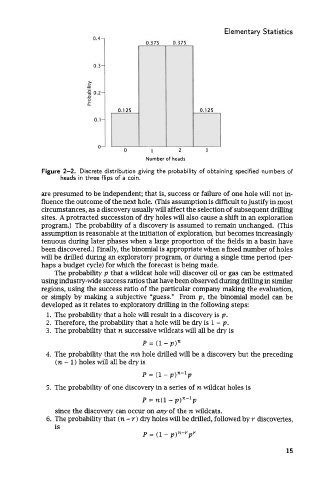
Number of heads

Figure 2-2. Discrete distribution giving the probability of obtaining specified numbers of
heads in three flips of a coin.

are presumed to be independent; that is, success or failure of one hole will not in-
fluence the outcome of the next hole. (This assumption is difficult to justify in most
circumstances, as a discovery usually will affect the selection of subsequent drilling
sites. A protracted succession of dry holes will also cause a shift in an exploration
program.) The probability of a discovery is assumed to remain unchanged. (This
assumption is reasonable at the initiation of exploration, but becomes increasingly
tenuous during later phases when a large proportion of the fields in a basin have
been discovered.) Finally, the binomial is appropriate when a fixed number of holes
will be drilled during an exploratory program, or during a single time period (per-
haps a budget cycle) for which the forecast is being made.
The probability p that a wildcat hole will discover oil or gas can be estimated
using industry-wide success ratios that have been observed during drilling in similar
regions, using the success ratio of the particular company making the evaluation,
or simply by making a subjective “guess.” From p, the binomial model can be
developed as it relates to exploratory drilling in the following steps:
1. The probability that a hole will result in a discovery is p.
2. Therefore, the probability that a hole will be dry is 1 - p.
3. The probability that n successive wildcats will all be dry is

P = (1 - p)n
4. The probability that the nth hole drilled will be a discovery but the preceding
(n - 1) holes will all be dry is

P = (1 - p)%-lp
5. The probability of one discovery in a series of n wildcat holes is
P = n(1- p)n-lp
since the discovery can occur on any of the n wildcats.
6. The probability that (n - Y) dry holes will be drilled, followed by Y discoveries,
is
P = (1 - ,)n-vpr

15