Page 119 - The Mechatronics Handbook

0066_Frame_C08 Page 10 Wednesday, January 9, 2002 3:48 PM

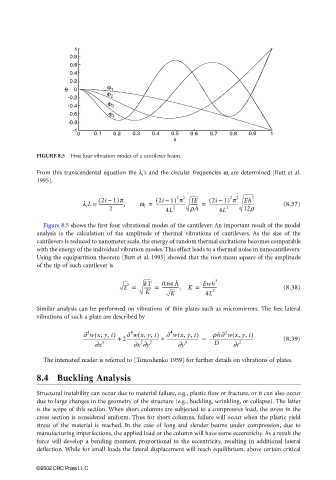
FIGURE 8.5 First four vibration modes of a cantilever beam.

From this transcendental equation the λ i ’s and the circular frequencies ω i are determined [Butt et al.
1995].

( 2i 1)p ( 2i 1) p 2 IE ( 2i 1) p 2 Eh 2
2
2
–
–
–
l i L ≅ ----------------------, w i = -------------------------- ------- = -------------------------- --------- (8.37)
2 4L 2 rA 4L 2 12r
Figure 8.5 shows the first four vibrational modes of the cantilever. An important result of the modal
analysis is the calculation of the amplitude of thermal vibrations of cantilevers. As the size of the
cantilevers is reduced to nanometer scale, the energy of random thermal excitations becomes comparable
with the energy of the individual vibration modes. This effect leads to a thermal noise in nanocantilevers.
Using the equipartition theorem [Butt et al. 1995] showed that the root mean square of the amplitude
of the tip of such cantilever is

------ =
z ˆ = kT 0.64 Å K = Ewh 3 (8.38)
2
------------
---------------,
K K 4L 2
Similar analysis can be performed on vibrations of thin plates such as micromirrors. The free lateral
vibrations of such a plate are described by
(
∂ wx, y, t) ∂ wx, y, t( ) ∂ wx, y, t( ) rh∂ wx, y, t( )
2
4
4
4
----------------------------- + 2----------------------------- + ----------------------------- = – ----------------------------------- (8.39)
2
∂x 4 ∂x ∂y 2 ∂y 4 D ∂t 2
The interested reader is referred to [Timoshenko 1959] for further details on vibrations of plates.
8.4 Buckling Analysis
Structural instability can occur due to material failure, e.g., plastic flow or fracture, or it can also occur
due to large changes in the geometry of the structure (e.g., buckling, wrinkling, or collapse). The latter
is the scope of this section. When short columns are subjected to a compressive load, the stress in the
cross section is considered uniform. Thus for short columns, failure will occur when the plastic yield
stress of the material is reached. In the case of long and slender beams under compression, due to
manufacturing imperfections, the applied load or the column will have some eccentricity. As a result the
force will develop a bending moment proportional to the eccentricity, resulting in additional lateral
deflection. While for small loads the lateral displacement will reach equilibrium, above certain critical

©2002 CRC Press LLC