Page 702 - The Mechatronics Handbook

0066_Frame_C23 Page 10 Wednesday, January 9, 2002 1:52 PM

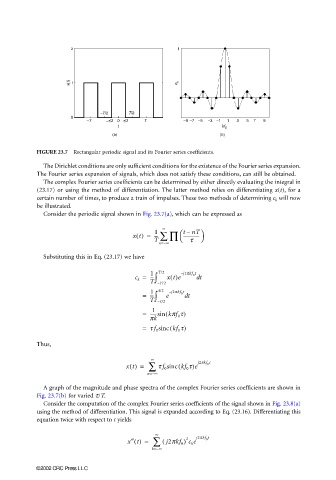
FIGURE 23.7 Rectangular periodic signal and its Fourier series coefficients.

The Dirichlet conditions are only sufficient conditions for the existence of the Fourier series expansion.
The Fourier series expansion of signals, which does not satisfy these conditions, can still be obtained.
The complex Fourier series coefficients can be determined by either directly evaluating the integral in
(23.17) or using the method of differentiation. The latter method relies on differentiating x(t), for a
certain number of times, to produce a train of impulses. These two methods of determining c k will now
be illustrated.
Consider the periodic signal shown in Fig. 23.7(a), which can be expressed as

∞
1
–
xt() = --- ∑ ∏  tnT 
--------------
T n=∞  τ 
–
Substituting this in Eq. (23.17) we have
c k = 1 ∫ T/2 xt()e – j2πkf t t d
0
---
T – T/2
= 1 ∫ τ/2 e – j2πkf t t d
0
---
T – τ/2
1
= ------sin kπf 0 τ( )
πk
= τ f 0 sinc kf 0 τ)
(
Thus,
∞
(
xt() = ∑ τ f 0 sinc kf 0 τ)e j2πkf t
0
n=∞
–
A graph of the magnitude and phase spectra of the complex Fourier series coefficients are shown in
Fig. 23.7(b) for varied τ/T.
Consider the computation of the complex Fourier series coefficients of the signal shown in Fig. 23.8(a)
using the method of differentiation. This signal is expanded according to Eq. (23.16). Differentiating this
equation twice with respect to t yields

∞
2
x″ t() = ∑ ( j2πkf 0 ) c k e j2πkf t
0
k=∞
–
©2002 CRC Press LLC