Page 700 - The Mechatronics Handbook

0066_Frame_C23 Page 8 Wednesday, January 9, 2002 1:52 PM

TABLE 23.2 Properties of the Correlation Function
Property Autocorrelation Crosscorrelation
Even/Reorder R xx t() = R xx –() R xy t() = R yx –()
t
t
Upper Bound R xx 0() ≥ R xx t() , for any t R xy t() ≤ R xx 0()R yy 0()

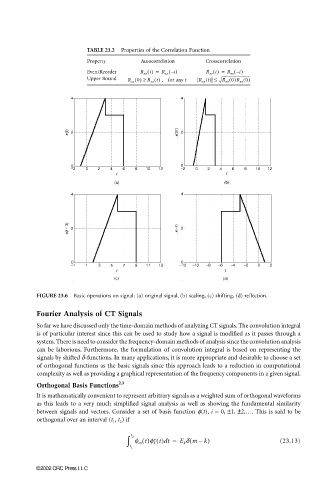
FIGURE 23.6 Basic operations on signal: (a) original signal, (b) scaling, (c) shifting, (d) reflection.

Fourier Analysis of CT Signals

So far we have discussed only the time-domain methods of analyzing CT signals. The convolution integral
is of particular interest since this can be used to study how a signal is modified as it passes through a
system. There is need to consider the frequency-domain methods of analysis since the convolution analysis
can be laborious. Furthermore, the formulation of convolution integral is based on representing the
signals by shifted δ-functions. In many applications, it is more appropriate and desirable to choose a set
of orthogonal functions as the basic signals since this approach leads to a reduction in computational
complexity as well as providing a graphical representation of the frequency components in a given signal.
Orthogonal Basis Functions 2,3
It is mathematically convenient to represent arbitrary signals as a weighted sum of orthogonal waveforms
as this leads to a very much simplified signal analysis as well as showing the fundamental similarity
between signals and vectors. Consider a set of basis function φ(t), i = 0, ±1, ±2,…. This is said to be
orthogonal over an interval (t 1 , t 2 ) if

∫ t 2 φ m t()φ k t() t = E k δ mk) (23.13)
(
∗
–
d
t 1
©2002 CRC Press LLC