Page 107 - Theory and Design of Air Cushion Craft

Air cushion wave-making drag 91

. a'/a=0.90
2.0

1.5

1.0

1
1 2a' 1
1 1
0.5

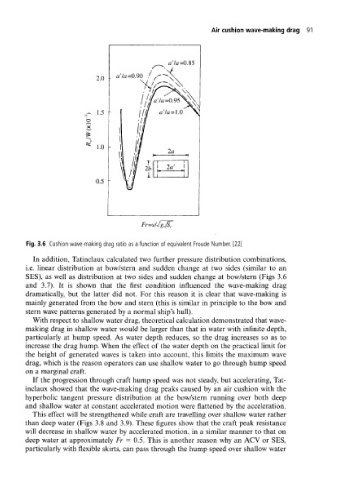
Fig. 3.6 Cushion wave-making drag ratio as a function of equivalent Froude Number. [22]
In addition, Tatinclaux calculated two further pressure distribution combinations,
i.e. linear distribution at bow/stern and sudden change at two sides (similar to an
SES), as well as distribution at two sides and sudden change at bow/stern (Figs 3.6
and 3.7). It is shown that the first condition influenced the wave-making drag
dramatically, but the latter did not. For this reason it is clear that wave-making is
mainly generated from the bow and stern (this is similar in principle to the bow and
stern wave patterns generated by a normal ship's hull).
With respect to shallow water drag, theoretical calculation demonstrated that wave-
making drag in shallow water would be larger than that in water with infinite depth,
particularly at hump speed. As water depth reduces, so the drag increases so as to
increase the drag hump. When the effect of the water depth on the practical limit for
the height of generated waves is taken into account, this limits the maximum wave
drag, which is the reason operators can use shallow water to go through hump speed
on a marginal craft.
If the progression through craft hump speed was not steady, but accelerating, Tat-
inclaux showed that the wave-making drag peaks caused by an air cushion with the
hyperbolic tangent pressure distribution at the bow/stern running over both deep
and shallow water at constant accelerated motion were flattened by the acceleration.
This effect will be strengthened while craft are travelling over shallow water rather
than deep water (Figs 3.8 and 3.9). These figures show that the craft peak resistance
will decrease in shallow water by accelerated motion, in a similar manner to that on
deep water at approximately Fr = 0.5. This is another reason why an ACV or SES,
particularly with flexible skirts, can pass through the hump speed over shallow water