Page 129 - Theory and Design of Air Cushion Craft

Sidewall wave-making drag 113

Yim [30] calculated the wave-making drag due to sidewalls by means of an even
simpler method. He considered that the total wave-making of an SES would be equal
to that of an ACV with the same cushion length and beam, i.e. it was considered that
the sidewalls did not provide any buoyancy, and the total craft weight would be sup-
ported only by an air cushion as to lead the same wave-making due to this equivalent
air cushion. The effective wave-making drag coefficient of the sidewalls calculated by
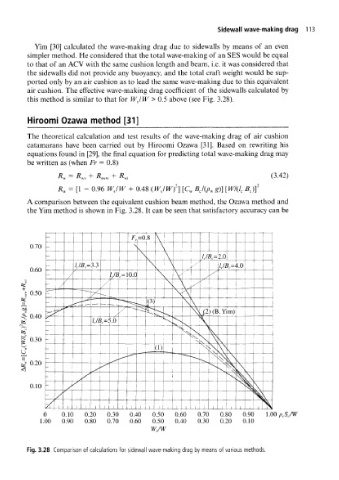
this method is similar to that for WJW > 0.5 above (see Fig. 3.28).

Hiroomi Ozawa method [31]

The theoretical calculation and test results of the wave-making drag of air cushion
catamarans have been carried out by Hiroomi Ozawa [31]. Based on rewriting his
equations found in [29], the final equation for predicting total wave-making drag may
be written as (when Fr = 0.8)
R», — R,,,, + R c + (3.42)
2
V = [1 - 0.96 WJW + 0.48 (WJW) } [C w B c/(p v gj\ [Wl(l c B c)] :
A comparison between the equivalent cushion beam method, the Ozawa method and
the Yim method is shown in Fig. 3.28. It can be seen that satisfactory accuracy can be

0.70 -

0 0.10 0.20 0.30 0.40 0.50 0.60 0.70 0.80 0.90 1.00 p cS c/W
1.00 0.90 0.80 0.70 0.60 0.50 0.40 0.30 0.20 0.10
WJW

Fig. 3.28 Comparison of calculations for sidewall wave-making drag by means of various methods.