Page 130 - Theory and Design of Air Cushion Craft

114 Steady drag forces

obtained by the equivalent method in the case of WJW < 0.2, but the wave-making
drag of sidewalls and its interference drag with the air cushion have to be taken into
account as WJW increases.
In conclusion, the methods for estimating sidewall drag introduced here are suitable
for SES with sidewall displacement up to about 30% of craft total weight. Where a
larger proportion of craft weight is borne by the sidewalls, the sidehull wave-making
should be considered directly, rather than as a 'correction' to the cushion wave-
making. Below 70% contribution to support from the air cushion, the beneficial effect
of the cushion itself rapidly dies away, and so it is more likely that optimizing cata-
maran hulls will achieve the designer's requirements in the speed range to 40 knots.
Above this speed, an air cushion supporting most of the craft weight is most likely to
give the optimum design with minimum powering.

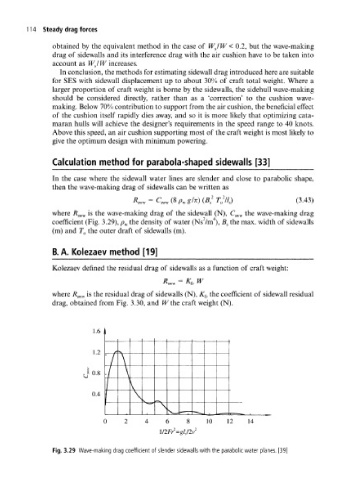
Calculation method for parabola-shaped sidewalls [33]

In the case where the sidewall water lines are slender and close to parabolic shape,
then the wave-making drag of sidewalls can be written as
(8 Av gin) (B s T 0 // s) (3.43)
where R^ is the wave-making drag of the sidewall (N), C sww the wave-making drag
coefficient (Fig. 3.29), p w the density of water (Ns"/m ), B s the max. width of sidewalls
(m) and T 0 the outer draft of sidewalls (m).

B. A. Kolezaev method [19]

Kolezaev defined the residual drag of sidewalls as a function of craft weight:

where R^ is the residual drag of sidewalls (N), K fr the coefficient of sidewall residual
drag, obtained from Fig. 3.30, and IV the craft weight (N).

1.6

10 12 14
2
l/2Fr =g/ s/2v 2
Fig. 3.29 Wave-making drag coefficient of slender sidewalls with the parabolic water planes. [39]