Page 293 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

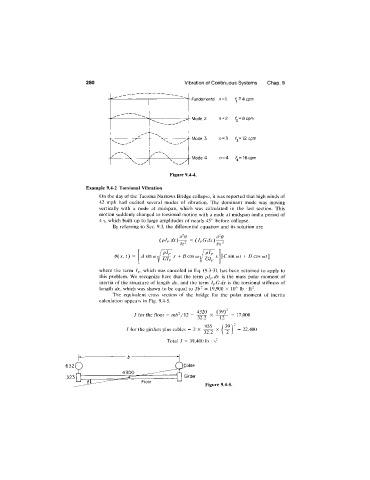
280 Vibration of Continuous Systems Chap. 9

Fundamental n =] f,=4cpm

Mode 2 n =2

Mode 3 n = 3 f,= 12cpm

Mode 4 n = 4

Figure 9.4-4.
Example 9.4-2 Torsional Vibration
On the day of the Tacoma Narrows Bridge collapse, it was reported that high winds of
42 mph had excited several modes of vibration. The dominant mode was moving
vertically with a node at midspan, which was calculated in the last section. This
motion suddenly changed to torsional motion with a node at midspan and a period of
4 s, which built up to large amplitudes of nearly 45° before collapse.
By referring to Sec. 9.3, the differential equation and its solution are
d^e
{ p l p d x ) ^ = {IpGdx) ^
J ?
/ ^P pJp
e {x , t ) = yf sin wi/ jc + B cos ( [C sin (ot D cos cot]
GIp
where the term Ip, which was. canceled in Eq. (9.3-3), has been retained to apply to
this problem. We recognize here that the term pIp dx is the mass polar moment of
inertia of the structure of length dx, and the term I p G dx is the torsional stiffness of
length dx, which was shown to be equal to Tb^ = 19,900 X 10^ lb • ft^.
The equivalent cross section of the bridge for the polar moment of inertia
calculation appears in Fig. 9.4-5.
4320 (39)^
J for the floor = mh^/\2 = - 17,000
32.2 12
955 / 39 2
J for the girders plus cables = 2 X ^ ^ ^ | ^ 400
Total J - 39,400 lb • s^

Figure 9.4-5.