Page 70 - Thomson, William Tyrrell-Theory of Vibration with Applications-Taylor _ Francis (2010)

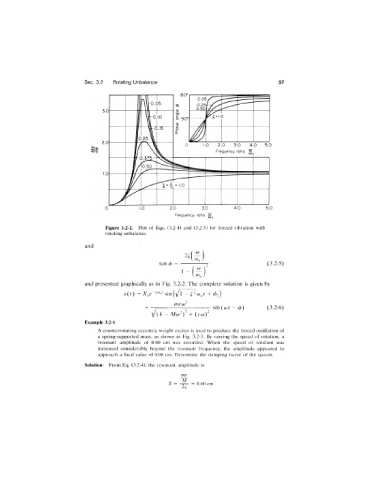
Sec. 3.2 Rotating Unbalance 57

Figure 3.2-2. Plot of Eqs. (3.2-4) and (3.2-5) for forced vibration with
rotating unbalance.
and
2^1 —
tan (j) (3.2-5)
1 - 1 ^
and presented graphically as in Fig. 3.2-2. The complete solution is given by
x{t) = sin |\ / l - + (/>, j
meco^
+ sin {(ot - (f)) (3.2-6)
] / { k - Moj-y + (Ciof
Example 3.2-1
A counterrotating eccentric weight exciter is used to produce the forced oscillation of
a spring-supported mass, as shown in Fig. 3.2-3. By varying the speed of rotation, a
resonant amplitude of 0.60 cm was recorded. When the speed of rotation was
increased considerably beyond the resonant frequency, the amplitude appeared to
approach a fixed value of 0.08 cm. Determine the damping factor of the system.
Solution: From Fq. (3.2-4), the resonant amplitude is
m e
~W
A = = 0.60 cm