Page 444 - Bird R.B. Transport phenomena

426 Chapter 14 Interphase Transport in Nonisothermal Systems

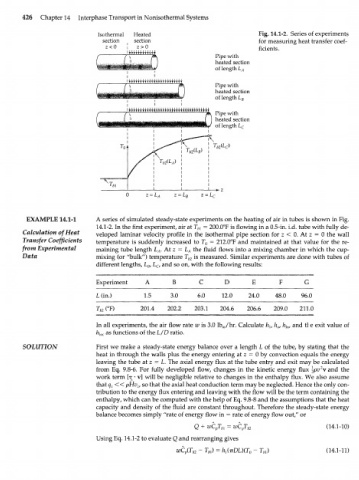
Isothermal Heated Fig. 14.1-2. Series of experiments
section ( section for measuring heat transfer coef-
2 < 0 ! 2 > 0 ficients.
Pipe with
heated section
of length L A

Pipe with
heated section
of length L
B
Pipe with
heated section
of length L
c

0 z = L A Z = L R Z = L C

EXAMPLE 14.1-1 A series of simulated steady-state experiments on the heating of air in tubes is shown in Fig.
14.1-2. In the first experiment, air at T = 200.0°F is flowing in a 0.5-in. i.d. tube with fully de-
h]
Calculation of Heat veloped laminar velocity profile in the isothermal pipe section for z < 0. At z = 0 the wall
Transfer Coefficients temperature is suddenly increased to T = 212.0°F and maintained at that value for the re-
o
from Experimental maining tube length L . At z = L A the fluid flows into a mixing chamber in which the cup-
A
Data mixing (or "bulk") temperature T b2 is measured. Similar experiments are done with tubes of
different lengths, L , L , and so on, with the following results:
c
B
Experiment A В С D E F G
L (in.) 1.5 3.0 6.0 12.0 24.0 48.0 96.0
T (°F) 201.4 202.2 203.1 204.6 206.6 209.0 211.0
h2
In all experiments, the air flow rate w is 3.0 lb,, /hr. Calculate h u h , h , and tl e exit value of
7
]n
a
h ]oc as functions of the L/D ratio.
SOLUTION First we make a steady-state energy balance over a length L of the tube, by stating that the
heat in through the walls plus the energy entering at z = 0 by convection equals the energy
leaving the tube at z = L. The axial energy flux at the tube entry and exit may be calculated
2
from Eq. 9.8-6. For fully developed flow, changes in the kinetic energy flux ^pi; v and the
work term [т • v] will be negligible relative to changes in the enthalpy flux. We also assume
that q z « pHv , so that the axial heat conduction term may be neglected. Hence the only con-
z
tribution to the energy flux entering and leaving with the flow will be the term containing the
enthalpy, which can be computed with the help of Eq. 9.8-8 and the assumptions that the heat
capacity and density of the fluid are constant throughout. Therefore the steady-state energy
balance becomes simply "rate of energy flow in = rate of energy flow out," or

Q + wC T bl = wC T b2 (14.1-10)
p
p
Using Eq. 14.1-2 to evaluate Q and rearranging gives
- Г ) (14.1-11)
0 м