Page 449 - Bird R.B. Transport phenomena

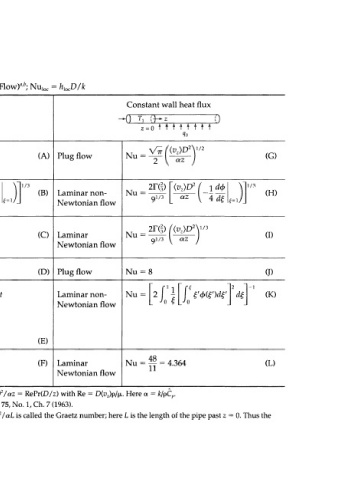
Table 14.2-1 Asymptotic Results for Local Nusselt Numbers (Tube Flow)"'*; Nu = h D/k
7
loc loc
Constant wall temperature Constant wall heat flux

-4) т, : > ;)
All values are z -4)
local Nu numbers z = 0 = 0 t t t t t t t f

1/2
Thermal entrance Plug flow (A) Plug flow Nu = (G)
region c

(v )D 2 2Г(|) [(v )D 2
z
•» 1 Laminar non- Nu = - z (B) Laminar non- Nu = (H)
az 91/3
Newtonian flow Newtonian flow

2Г(р l/3
Laminar Nu = 1/3 (C) Laminar Nu = 91/3 (I)
Newtonian flow 9 Г© Newtonian flow

Plug flow Nu = 5.772 (D) Plug flow Nu = (J)

Thermally fully Laminar non- Nu = 0\, where /^ is the lowest Laminar non-
developed flow Newtonian flow eigenvalue of Newtonian flow

« 1
az
x
x; (o) = o, (i) = о (E)
7 n
Laminar Nu = 3.657 (F) Laminar Nu = Ц = 4.364 (L)
Newtonian flow Newtonian flow

a 2
Note: ФШ = v /{v ), where ^ = r/R and R = D/2; for Newtonian fluids (v )D /az = RePr(D/z) with Re = D<y>p/(JL. Here a = k/pC .
z z z z p
" W. J. Beek and R. Eggink, De Ingenieur, 74, No. 35, Ch. 81-89 (1962); erratum, 75, No. 1, Ch. 7 (1963).
The grouping (v )D /az is sometimes written as Gz • (L/z) where Gz = (v )D /aL is called the Graetz number; here L is the length of the pipe past 2 = 0. Thus the
c 2 2
z
z
thermal entry region corresponds to large Graetz number.