Page 452 - Bird R.B. Transport phenomena

432 Chapter 14 Interphase Transport in Nonisothermal Systems

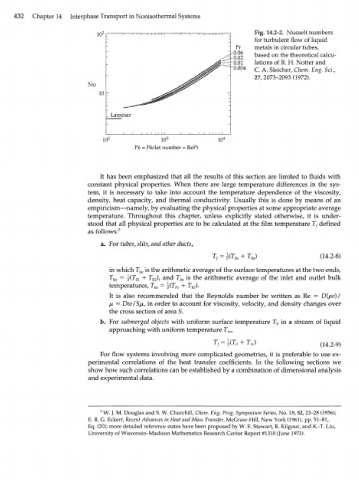
Fig. 14.2-2. Nusselt numbers
for turbulent flow of liquid
metals in circular tubes,
based on the theoretical calcu-
lations of R. H. Notter and
C. A. Sleicher, Chem. Eng, ScL,
27,2073-2093(1972).

10 2 10 3 10 4
Pe = Peclet number = RePr

It has been emphasized that all the results of this section are limited to fluids with
constant physical properties. When there are large temperature differences in the sys-
tem, it is necessary to take into account the temperature dependence of the viscosity,
density, heat capacity, and thermal conductivity. Usually this is done by means of an
empiricism—namely, by evaluating the physical properties at some appropriate average
temperature. Throughout this chapter, unless explicitly stated otherwise, it is under-
stood that all physical properties are to be calculated at the film temperature T f defined
as follows: 5
a. For tubes, slits, and other ducts,
(14.2-8)

in which T Oa is the arithmetic average of the surface temperatures at the two ends,
Ton = l(T 0l + T 02), and T ba is the arithmetic average of the inlet and outlet bulk
temperatures, T ba = \{J bl + T b2).
It is also recommended that the Reynolds number be written as Re = D(pv)/
IJL = DW/S/JL, in order to account for viscosity, velocity, and density changes over
the cross section of area S.
bo For submerged objects with uniform surface temperature T o in a stream of liquid
approaching with uniform temperature T*,,
Tf = i(T 0 + To») (14.2-9)
For flow systems involving more complicated geometries, it is preferable to use ex-
perimental correlations of the heat transfer coefficients. In the following sections we
show how such correlations can be established by a combination of dimensional analysis
and experimental data.

5
W. J. M. Douglas and S. W. Churchill, Chem. Eng. Prog. Symposium Series, No. 18, 52, 23-28 (1956);
E. R. G. Eckert, Recent Advances in Heat and Mass Transfer, McGraw-Hill, New York (1961), pp. 51-81,
Eq. (20); more detailed reference states have been proposed by W. E. Stewart, R. Kilgour, and K.-T. Liu,
University of Wisconsin-Madison Mathematics Research Center Report #1310 (June 1973).