Page 447 - Bird R.B. Transport phenomena

§14.2 Analytical Calculations of Heat Transfer Coefficients for Forced Convection Through Tubes and Slits 429

(v z )D 2 (v z )B 2
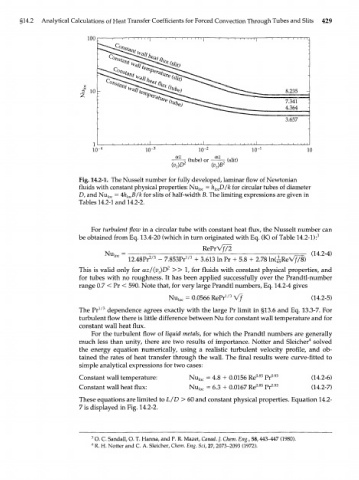
Fig. 14.2-1. The Nusselt number for fully developed, laminar flow of Newtonian
fluids with constant physical properties: Nu foc = h D/k for circular tubes of diameter
loc
D, and Nu ]oc = 4h B/k for slits of half-width B. The limiting expressions are given in
]oc
Tables 14.2-1 and 14.2-2.

For turbulent flow in a circular tube with constant heat flux, the Nusselt number can
be obtained from Eq. 13.4-20 (which in turn originated with Eq. (K) of Table 14.2-1): 3
RePrVf/2
N u = (14.2-4)
lo w c 2/3 1/3
12.48Рг - 7.853Рг + 3.613 In Pr + 5.8 + 2.78 ln(^ReVf/8)
This is valid only for az/(v )D 2 » 1, for fluids with constant physical properties, and
z
for tubes with no roughness. It has been applied successfully over the Prandtl-number
range 0.7 < Pr < 590. Note that, for very large Prandtl numbers, Eq. 14.2-4 gives
1/3
Nu loc = 0.0566 RePr V/ (14.2-5)
1/ 3
The Pr dependence agrees exactly with the large Pr limit in §13.6 and Eq. 13.3-7. For
turbulent flow there is little difference between Nu for constant wall temperature and for
constant wall heat flux.
For the turbulent flow of liquid metals, for which the Prandtl numbers are generally
much less than unity, there are two results of importance. Notter and Sleicher 4 solved
the energy equation numerically, using a realistic turbulent velocity profile, and ob-
tained the rates of heat transfer through the wall. The final results were curve-fitted to
simple analytical expressions for two cases:

Constant wall temperature: Nu = 4.8 + 0.0156 Re 08 5 Pr 09 3 (14.2-6)
loc
0 93
0 85
Constant wall heat flux: Nu = 6.3 + 0.0167 Re - Pr - (14.2-7)
loc
These equations are limited to L/D > 60 and constant physical properties. Equation 14.2-
7 is displayed in Fig. 14.2-2.

3
О. С Sandall, O. T. Hanna, and P. R. Mazet, Canad. }. Chem. Eng., 58, 443-447 (1980).
4
R. H. Notter and С A. Sleicher, Chem. Eng. Sci, 27, 2073-2093 (1972).