Page 445 - Bird R.B. Transport phenomena

§14.1 Definitions of Heat Transfer Coefficients 427

from which
_ wCp (T b2 - T b1) / p
(14.1-12)
1 2
TTD ( T 0 - T M ) U
This gives us the formula for calculating h } from the data given above.
Analogously, use of Eqs. 14.1-3 and 14.1-4 gives
, _ «>Cp (T b2 ~ T bl) p
/
2 (14.1-13)
" TTD (T 0 -T b ) a \L
= (14.1-14)
h ln 2
TTD (T o -
for obtaining h a and h [n from the data.
To evaluate /z Ioc , we have to use the preceding data to construct a continuous curve T b(z),
as in Fig. 14.1-2, to represent the change in bulk temperature with z in the longest (96-in.)
tube. Then Eq. 14.1-10 becomes
Q(z) = wC pT b(z) (14.1-15)
By differentiating this expression with respect to z and combining the result with Eq. 14.1-5,
we get
dT h
-± = - T b)
wC p /j loc7rD(7 0 (14.1-16)
or
™Cy 1 dT b
(14.1-17)
TTD (T O - T b) dz
Since T o is constant, this becomes

™C pd\n(T 0-T b)( D
^loc 2 (14.1-18)
TTD d(z/L) \L
The derivative in this equation is conveniently determined from a plot of ln(T 0 - T b) versus
z/L. Because a differentiation is involved, it is difficult to determine /z loc precisely.
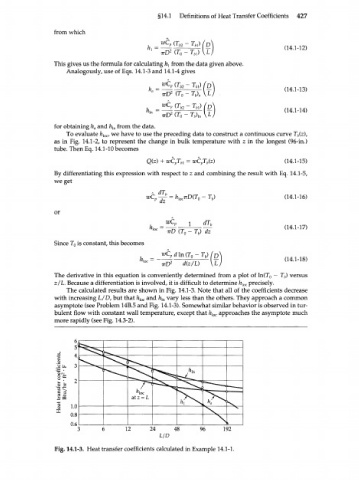
The calculated results are shown in Fig. 14.1-3. Note that all of the coefficients decrease
with increasing L/D, but that h Xoc and h Xn vary less than the others. They approach a common
asymptote (see Problem 14B.5 and Fig. 14.1-3). Somewhat similar behavior is observed in tur-
bulent flow with constant wall temperature, except that h ]oc approaches the asymptote much
more rapidly (see Fig. 14.3-2).

192

Fig. 14.1-3. Heat transfer coefficients calculated in Example 14.1-1.