Page 542 - Bird R.B. Transport phenomena

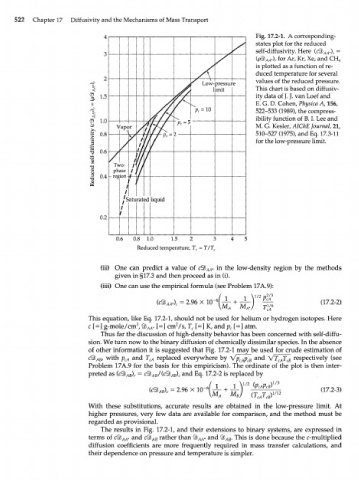
522 Chapter 17 Diffusivity and the Mechanisms of Mass Transport

Fig. 17.2-1. A corresponding-
states plot for the reduced
self-diffusivity. Here {сЯЬ *) г =
АА
{рЯЬ *) for Ar, Kr, Xe, and CH 4
г
АА
is plotted as a function of re-
duced temperature for several
values of the reduced pressure.
This chart is based on diffusiv-
ity data of J. J. van Loef and
E. G. D. Cohen, Physica A, 156,
522-533 (1989), the compress-
ibility function of B. I. Lee and
M. G. Kesler, AIChE Journal, 21,
510-527 (1975), and Eq. 17.3-11
for the low-pressure limit.

0.6 0.8 1.0 1.5 2 3
Reduced temperature, T r = T/T c

(ii) One can predict a value of СЯЬАА* in the low-density region by the methods
given in §17.3 and then proceed as in (i).
(iii) One can use the empirical formula (see Problem 17A.9):
1/2
^ = 2 . 9 6 X 1 0 - ^ (17.2-2)

This equation, like Eq. 17.2-1, should not be used for helium or hydrogen isotopes. Here
2
3
с [=] g-mole/cm ,2) * [=] cm /s, T [=] K, and p [=] atm.
ЛЛ c c
Thus far the discussion of high-density behavior has been concerned with self-diffu-
sion. We turn now to the binary diffusion of chemically dissimilar species. In the absence
of other information it is suggested that Fig. 17.2-1 may be used for crude estimation of
сЯЬ , with p and T replaced everywhere by Vp p and VT T respectively (see
АВ cA cA cA cB cA cB
Problem 17A.9 for the basis for this empiricism). The ordinate of the plot is then inter-
preted as (c% ) = сЯЬ /(сЯЬ ) and Eq. 17.2-2 is replaced by
AB r АВ АВ с
(c% ) - 2.96 X 10 [ +Jf B ^
WA
AB c
With these substitutions, accurate results are obtained in the low-pressure limit. At
higher pressures, very few data are available for comparison, and the method must be
regarded as provisional.
The results in Fig. 17.2-1, and their extensions to binary systems, are expressed in
terms of сЯЬ * and c4b rather than ЯЬ^* and ЯЬ . This is done because the c-multiplied
АВ
AB
АА
diffusion coefficients are more frequently required in mass transfer calculations, and
their dependence on pressure and temperature is simpler.