Page 572 - Bird R.B. Transport phenomena

552 Chapter 18 Concentration Distributions in Solids and in Laminar Flow
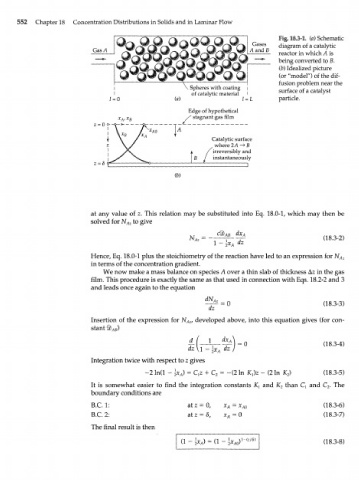
Fig. 18.3-1. (a) Schematic
diagram of a catalytic
reactor in which A is
being converted to B.
(b) Idealized picture
(or "model") of the dif-
fusion problem near the
Spheres with coating | surface of a catalyst
of catalytic material I
1 = 0 (a) 1 = 1 particle.
Edge of hypothetical
X stagnant gas film

Catalytic surface
where 2 A -> В
irreversibly and
instantaneously
1
(b)

at any value of z. This relation may be substituted into Eq. 18.0-1, which may then be
solved for N Az to give
dx
N* = -- A (18.3-2)
- \x dz
A
Hence, Eq. 18.0-1 plus the stoichiometry of the reaction have led to an expression for N
Az
in terms of the concentration gradient.
We now make a mass balance on species A over a thin slab of thickness Az in the gas
film. This procedure is exactly the same as that used in connection with Eqs. 18.2-2 and 3
and leads once again to the equation
dN
Az = 0 (18.3-3)
dz
Insertion of the expression for N Az/ developed above, into this equation gives (for con-
stant ЯЬ )
АВ
d 1 dx, = 0 (18.3-4)
dz Vl - \x dz
A
Integration twice with respect to z gives
-2 ln(l - \x ) = Qz + C = -(2 In K )z - (2 In K ) (18.3-5)
A 2 x 2
It is somewhat easier to find the integration constants K^ and K 2 than Q and C . The
2
boundary conditions are
B.C. 1: at z = o, X 'A = x A 0 (18.3-6)
B.C. 2: at z = 8, лA = 0 (18.3-7)
The final result is then
(1 - hсл) = (1 - 2 A0> (18.3-8)
l
\\~(z/8)
X