Page 713 - Bird R.B. Transport phenomena

§22.4 Definition of Transfer Coefficients in Two Phases 693

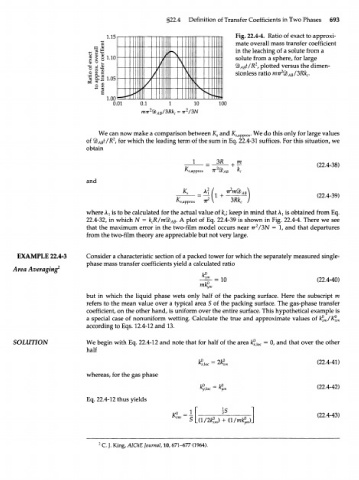
1.15 г— Fig. 22.4-4. Ratio of exact to approxi-
mate overall mass transfer coefficient
in the leaching of a solute from a
1.10 solute from a sphere, for large
\ 2
%b ABt/R , plotted versus the dimen-
l
s sionless ratio mTT 4l) AB/3Rk r
: £ 1.05
/ v
1.00
0.01 0.1 1 10 100
2 2
m7T 9) AB/3Rk c = T T / 3 N

We can now make a comparison between K s and K sapprox. We do this only for large values
2
of %b ABt/R , for which the leading term of the sum in Eq. 22.4-31 suffices. For this situation, we
obtain
1 3R
(22.4-38)
L
s,approx
and
(22.4-39)
К s^pprox
where A] is to be calculated for the actual value of k ; keep in mind that AT is obtained from Eq.
c
22.4-32, in which N = k R/m9) . A plot of Eq. 22.4-39 is shown in Fig. 22.4-4. There we see
c
AB
2
that the maximum error in the two-film model occurs near TT /3N = 1, and that departures
from the two-film theory are appreciable but not very large.
EXAMPLE 22.4-3 Consider a characteristic section of a packed tower for which the separately measured single-
phase mass transfer coefficients yield a calculated ratio
Area Averaging 2
A: 0
= 10 (22.4-40)
л
у«
but in which the liquid phase wets only half of the packing surface. Here the subscript m
refers to the mean value over a typical area S of the packing surface. The gas-phase transfer
coefficient, on the other hand, is uniform over the entire surface. This hypothetical example is
a special case of nonuniform wetting. Calculate the true and approximate values of k° /K? xw
xm
according to Eqs. 12.4-12 and 13.
SOLUTION We begin with Eq. 22.4-12 and note that for half of the area k° x Ioc = 0, and that over the other
half
(22.4-41)
whereas, for the gas phase
(22.4-42)

Eq. 22.4-12 thus yields
* =i[ i5 1 (22.4-43)

"™ S Ul/210 + (l/ffl*»)J

2
C. J. King, AlChE Journal, 10, 671-677 (1964).