Page 34 - Using ANSYS for Finite Element Analysis A Tutorial for Engineers

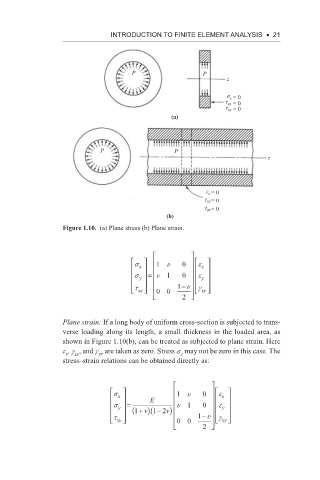
IntroductIon to FInIte element AnAlysIs • 21

P P
z

σ = 0
τ xz x = 0
τ zy = 0
(a)

P P
z

ε z = 0
γ zx = 0
γ yz = 0
(b)
Figure 1.10. (a) Plane stress (b) Plane strain.

 
 s  1 u 0   e 
 x     x 
s  y  =  u 1 0  e  y 
   − u   
  t xy   00 1     g xy  
 2 

Plane strain: If a long body of uniform cross-section is subjected to trans-
verse loading along its length, a small thickness in the loaded area, as
shown in Figure 1.10(b), can be treated as subjected to plane strain. Here
e , g , and g are taken as zero. Stress s may not be zero in this case. The
yz
z
z
zx
stress–strain relations can be obtained directly as:
 

 s  1 u 0  e 
e
 x  E    x 
s  y  =  u 1 0   e 
y
v) − 2
  (1 + (1 v)  − u   
  t xy   00 1    g xy  
 2 