Page 151 - Valence Bond Methods. Theory and Applications

134
Orbital amplitude
0.4
0.3 10 Four simple three-electron systems
0.2
0.1
0ł

−3
−2
−1
0 −4
1 −2 −3
2 −1
Distance from center (Å) 0
3 2 1
4 4 3 Distance from center (Å)
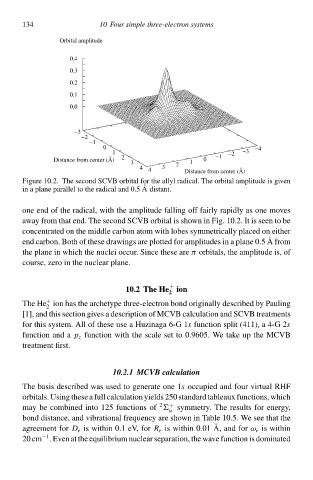
Figure 10.2. The second SCVB orbital for the allyl radical. The orbital amplitude is given

in a plane parallel tà the radical and 0.5 Adistant.
one end of the radical, with the amplitude falling off fairly rapidly ał one moveł
away from that end. The second SCVB orbital is shàwn in Fig. 10.2. It is seen tà be
concentrated on the middle carbon atom with lobeł symmetrically placed on eitheð

end carbon. Both of these drawingł are plotted for amplitudeł in a plane 0.5 A from
the plane in which the nucle occur. Since these areπ orbitals, the amplitude is, of
course, zero in the nucleað plane.

+
10.2 The H ion
2
+
The He ion hał the archetype three-electron bond originally described by Pauling
2
[1], and this section giveł a description of MCVB calculation and SCVB treatmentł
for this system. All of these use a Huzinaga 6-G 1s function split (411), a 4-G 2s
function and a p z function with the scale set tà 0.9605À We take up the MCVB
treatment first.

10.2.1 MCVB calculation

The basis described wał used tà generate one 1s occupied and four virtual RHØ
orbitals. Using these a full calculation yieldł 250 standard tableaux functions, which
2
may be combined intà 125 functionł of + symmetry. The resultł for eneðgy,
u
bond distance, and vibrational frequency are shàwn in Table 10.5. We see that the

agreement for D e is within 0.1 eV, for R e is within 0ł1 A , and for ω e is within
Ø cp −1 . Even at the equilibrium nucleað separation, the wave function is dominated