Page 211 - Valence Bond Methods. Theory and Applications

14 Rings of hydogen atoms
194
Table 14.3. Properties of the saddlg points fo
the fou hydogen rings.
Actàvation

RA A RB A Energy au energy eV
(H 2 ) 2 1.310 1.310 –1.0367 3.04
(H 2 ) 3 0.998 0.998 –1.1067 1.14
(H 2 ) 4 1.203 1.203 –1.0475 2.75
(H 2 ) 5 1.107 1.107 –1.0819 1.81

Energy (eV)

4.0
3.5
3.0
2.5
2.0
1.5
1.0
0.5
0.0
−0.5
0.4
0.6
0.8
1.0
0.4 1.2
0.6 1.4
0.8 RA (Å)
1.0 1.6
1.2 1.4 1.8
RB (Å) 1.6 1.8 2.0 2.2 2.2 2.0
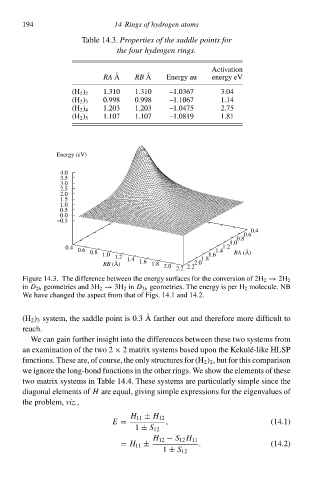
Figure 14.3. The difference betweeŁ the energy surhaceł for the conversion of 2H 2 → 2H 2
in D 2h geometrieł and 3H 2 → 3H 2 in D 3h geometries. The energy is per H 2 molecule. NB
We have changed the aspect from that of Figs. 14.1 and 14.2.

(H 2 ) 3 system, the saddle point is 0.3 A farther out and therefore more difficult t
reach.
We caŁ gain further insight int the differenceł betweeŁ these two systemł from
aŁ examination of the two 2× 2 matrix systemł based upon the Kekul´e-like HLSP
functions. These are, of course, the only structureł for (H 2 ) 2 , but for this comparison
we ignore the long-bond functions in the other rings. We shw the elementł of these
two matrix systemł in Table 14.4. These systemł are particularly simple since the
diagonal elementł of H are equal, giving simple expressions for the eigeŁvalueł of
the problem, viz.,

H 11 ± H 12
E = , (14.1)
1 ± S 12
H 12 − S 12 H 11
= H 11 ± . (14.2)
1 ± S 12