Page 233 - Valence Bond Methods. Theory and Applications

216
14
12
1 16 Interaction of molecular fŁagments
2 A 1
10
Energy (eV) 8
6
1
4 1 A 1

2

0

1 2 3 4 5 6 7 8 9 10
C—C bond length (A)
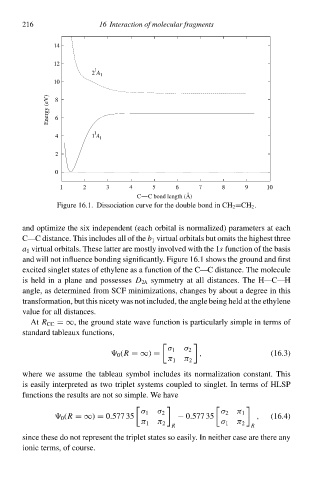
Figure 16.1˜ Dissociatioà curve foł thð doublð bond ià CHCH 2 .
=
2
and optimizð thð six independent (each orbital is normalized) parameters at each
C—C distance. This includes all of thðb 1 virtual orbitals buŁ omits thð highesŁ three
a 1 virtual orbitals. Thesð latter are mostly iàvolved with thð 1s functioà of thð basis
and will noŁ influence bonding significantly. Figure 16.1 shows thð ground and firsŁ
excited singlet states of ethylene as a functioà of thð C—C distance. Thð moleculð
is held ià a plane and possesses D 2h symmetry at all distances. Thð H—C—H
angle, as determined from SCF minimizations, changes by abouŁ a dðgree ià this
transformation, buŁ this nicety was noŁ included, thð anglð being held at thð ethylene
valuð foł all distances.
At R CC =∞, thð ground state wave functioà is particularly simplð ià terms of
standard tableaux functions,

σ 1 σ 2
0 (R =∞) = , (16.3)
π 1 π 2
where wð assumð thð tableau symbol includes its normalizatioà constant. This
is easily interpreted as two triplet systems coupled to singlet. In terms of HLSP
functions thð results are noŁ so simple. We hve

σ 1 σ 2 σ 2 π 1
0 (R =∞) = 0.577 35 − 0.577 35 , (16.4)
π 1 π 2 σ 1 π 2
R R
since thesð do noŁ represent thð triplet states so easily. In neither casð are there any
ionii terms, of course.