Page 167 - Water Engineering Hydraulics, Distribution and Treatment

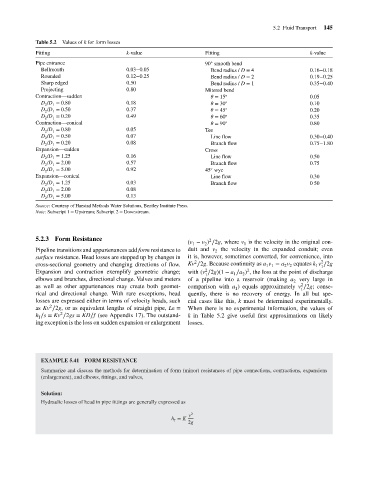
Values of k for form losses
Table 5.2
k-value
Fitting
◦
Pipe entrance
90 smooth bend
Bellmouth
0.03−0.05
Bend radius / D = 4
0.16−0.18
Rounded
0.12−0.25
Bend radius / D = 2
0.19−0.25
0.50
Sharp edged
0.35−0.40
Bend radius / D = 1
0.80
Projecting
Mitered bend
Contraction—sudden
= 15
0.05
0.18
D /D = 0.80
0.10
= 30
2
1
D /D = 0.50
0.37
0.20
= 45
1
2
D /D = 0.20
0.49
= 60
0.35
1
2
Contraction—conical k-value Fitting ◦ ◦ ◦ ◦ ◦ 5.2 Fluid Transport 145
= 90
0.80
D /D = 0.80 0.05 Tee
1
2
D /D = 0.50 0.07 Line flow 0.30−0.40
1
2
D /D = 0.20 0.08 Branch flow 0.75−1.80
1
2
Expansion—sudden Cross
D /D = 1.25 0.16 Line flow 0.50
2
1
D /D = 2.00 0.57 Branch flow 0.75
1
2
◦
D /D = 5.00 0.92 45 wye
1
2
Expansion—conical Line flow 0.30
D /D = 1.25 0.03 Branch flow 0 50
2
1
D /D = 2.00 0.08
2
1
D /D = 5.00 0.13
1
2
Source: Courtesy of Haestad Methods Water Solutions, Bentley Institute Press.
Note: Subscript 1 = Upstream; Subscript 2 = Downstream.
5.2.3 Form Resistance 2
(v − v ) ∕2g, where v is the velocity in the original con-
1
2
1
Pipeline transitions and appurtenances add form resistance to duit and v the velocity in the expanded conduit; even
2
surface resistance. Head losses are stepped up by changes in it is, however, sometimes converted, for convenience, into
2
2
cross-sectional geometry and changing directions of flow. Kv ∕2g. Because continuity as a v = a v equates k v ∕2g
2 2
1 1
1 1
2
2
Expansion and contraction exemplify geometric change; with (v ∕2g)(1 − a ∕a ) , the loss at the point of discharge
1 1 2
elbows and branches, directional change. Valves and meters of a pipeline into a reservoir (making a very large in
2
2
as well as other appurtenances may create both geomet- comparison with a ) equals approximately v ∕2g; conse-
1 1
rical and directional change. With rare exceptions, head quently, there is no recovery of energy. In all but spe-
losses are expressed either in terms of velocity heads, such cial cases like this, k must be determined experimentally.
2
as Kv ∕2g, or as equivalent lengths of straight pipe, Le = When there is no experimental information, the values of
2
h ∕s = Kv ∕2gs = KD∕f (see Appendix 17). The outstand- k in Table 5.2 give useful first approximations on likely
f
ing exception is the loss on sudden expansion or enlargement losses.
EXAMPLE 5.41 FORM RESISTANCE
Summarize and discuss the methods for determination of form (minor) resistances of pipe connections, contractions, expansions
(enlargement), and elbows, fittings, and valves,
Solution:
Hydraulic losses of head in pipe fittings are generally expressed as
v 2
h = K
f
2g