Page 56 - Fluid Power Engineering

34 Chapter Three

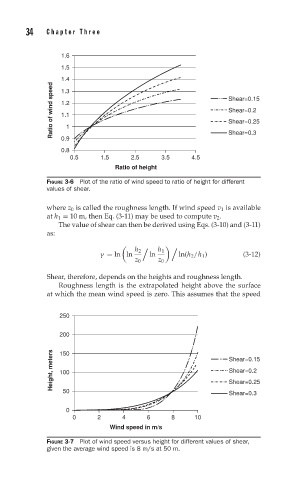
1.6
1.5
1.4
Ratio of wind speed 1.2 1 Shear=0.15
1.3

Shear=0.2
1.1
Shear=0.25

0.9
0.8 Shear=0.3
0.5 1.5 2.5 3.5 4.5
Ratio of height
FIGURE 3-6 Plot of the ratio of wind speed to ratio of height for different
values of shear.

where z 0 is called the roughness length. If wind speed v 1 is available
at h 1 = 10 m, then Eq. (3-11) may be used to compute v 2 .
The value of shear can then be derived using Eqs. (3-10) and (3-11)
as:

h 2
h 1
γ = ln ln ln ln(h 2 /h 1 ) (3-12)
z 0 z 0
Shear, therefore, depends on the heights and roughness length.
Roughness length is the extrapolated height above the surface
at which the mean wind speed is zero. This assumes that the speed

250

200
Height, meters 150 Shear=0.15

Shear=0.2
100
50 Shear=0.25
Shear=0.3
0
0 2 4 6 8 10
Wind speed in m/s
FIGURE 3-7 Plot of wind speed versus height for different values of shear,
given the average wind speed is 8 m/s at 50 m.