Page 292 - Wind Energy Handbook

266 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

(6) calculate first mode blade tip displacement, velocity and acceleration at end of
first time step, using Equations (5.86), (5.84) and (5.83) respectively (with i ¼ 1);

(7) repeat Stage 6 for each successive time step over several revolutions until
convergence achieved;

(8) calculate cyclic blade moment variation at radii of interest by multiplying the
cyclic tip displacement variation by appropriate factors derived from the modal
analysis;
(9) repeat Stages 6–8 for higher modes;

(10) combine the responses from different modes to obtain the total response.

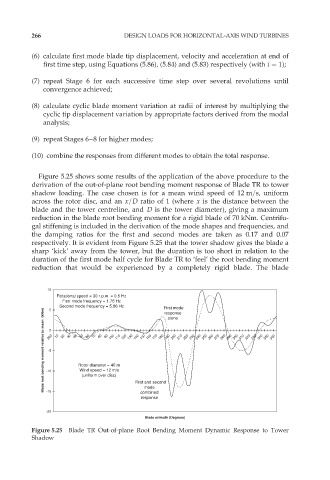
Figure 5.25 shows some results of the application of the above procedure to the
derivation of the out-of-plane root bending moment response of Blade TR to tower
shadow loading. The case chosen is for a mean wind speed of 12 m=s, uniform
across the rotor disc, and an x=D ratio of 1 (where x is the distance between the
blade and the tower centreline, and D is the tower diameter), giving a maximum
reduction in the blade root bending moment for a rigid blade of 70 kNm. Centrifu-
gal stiffening is included in the derivation of the mode shapes and frequencies, and
the damping ratios for the first and second modes are taken as 0.17 and 0.07
respectively. It is evident from Figure 5.25 that the tower shadow gives the blade a
sharp ‘kick’ away from the tower, but the duration is too short in relation to the
duration of the first mode half cycle for Blade TR to ‘feel’ the root bending moment
reduction that would be experienced by a completely rigid blade. The blade

10
Rotational speed = 30 r.p.m. = 0.5 Hz
First mode frequency = 1.78 Hz
Second mode frequency = 5.86 Hz First mode
Blade root bending moment relative to mean (kNm) -10 360 -5 0 10 20 30 40 Rotor diameter = 40 m 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300 310 320 330 340 350 360
5
response
alone
80
70
90
110
100
60
50
Wind speed = 12 m/s
(uniform over disc)
First and second
mode
-15
combined
response
-20
Blade azimuth (Degrees)
Figure 5.25 Blade TR Out-of-plane Root Bending Moment Dynamic Response to Tower
Shadow