Page 296 - Wind Energy Handbook

270 DESIGN LOADS FOR HORIZONTAL-AXIS WIND TURBINES

10000
Speed of rotation = 30 r.p.m. = 0.5 Hz
Mean wind speed = 8 m/s Power spectrum
Turbulence intensity = 12.5% of tip deflection
Integral length scale, L =73.5 m ignoring dynamic
1000 First mode natural frequency = 1.78 Hz magnification
(proportional to
spectrum of
nS y1 (n) (logarithmic scale) 100 spectrum of
generalized load)
Power
10
tip deflection
including
dynamic
magnification
1
Dynamic magnification ratio squared
based on damping ratio 0.1
0.1
0.01 0.1 1 10
Frequency, (Hz logarithmic scale)
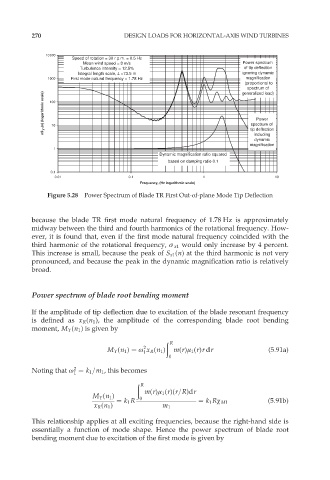
Figure 5.28 Power Spectrum of Blade TR First Out-of-plane Mode Tip Deflection

because the blade TR first mode natural frequency of 1.78 Hz is approximately
midway between the third and fourth harmonics of the rotational frequency. How-
ever, it is found that, even if the first mode natural frequency coincided with the
third harmonic of the rotational frequency, ó x1 would only increase by 4 percent.
This increase is small, because the peak of S x1 (n) at the third harmonic is not very
pronounced, and because the peak in the dynamic magnification ratio is relatively
broad.

Power spectrum of blade root bending moment

If the amplitude of tip deflection due to excitation of the blade resonant frequency
is defined as x R (n 1 ), the amplitude of the corresponding blade root bending
moment, M Y (n 1 ) is given by
ð R
2
M Y (n 1 ) ¼ ø x R (n 1 ) m(r)ì 1 (r)r dr (5:91a)
1
0
2
Noting that ø ¼ k 1 =m 1 , this becomes
1
ð
R
m(r)ì 1 (r)(r=R)dr
M Y (n 1 ) 0
¼ k 1 R ¼ k 1 R÷ M1 (5:91b)
x R (n 1 ) m 1
This relationship applies at all exciting frequencies, because the right-hand side is
essentially a function of mode shape. Hence the power spectrum of blade root
bending moment due to excitation of the first mode is given by