Page 268 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
P2: KVU/KXT
P1: KVU/KXT
QC: —/—
20:46
June 22, 2007
AT029-Manual-v7.cls
AT029-Manual
AT029-06
248 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
i in a mixture is shown by ¯ M i and is defined as
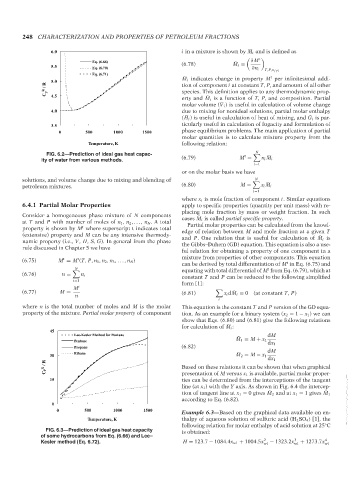
6.0
∂M t
Eq. (6.66)
5.5 Eq. (6.70) (6.78) ¯ M i =
∂n i
T,P,n j =i
Eq. (6.71)
¯ M i indicates change in property M per infinitesimal addi-
t
5.0
ig / R tion of component i at constant T, P, and amount of all other
C P 4.5 species. This definition applies to any thermodynamic prop-
erty and ¯ M i is a function of T, P, and composition. Partial
molar volume ( ¯ V i ) is useful in calculation of volume change
4.0 due to mixing for nonideal solutions, partial molar enthalpy
( ¯ H i ) is useful in calculation of heat of mixing, and ¯ G i is par-
3.5 ticularly useful in calculation of fugacity and formulation of
0 500 1000 1500 phase equilibrium problems. The main application of partial
molar quantities is to calculate mixture property from the
Temperature, K following relation:
N
FIG. 6.2—Prediction of ideal gas heat capac- t ¯
ity of water from various methods. (6.79) M = n i M i
i=1
or on the molar basis we have
solutions, and volume change due to mixing and blending of
N
¯
petroleum mixtures. (6.80) M = x i M i
i=1
where x i is mole fraction of component i. Similar equations
6.4.1 Partial Molar Properties apply to specific properties (quantity per unit mass) with re-
placing mole fraction by mass or weight fraction. In such
Consider a homogeneous phase mixture of N components cases ¯ M i is called partial specific property.
at T and P with number of moles of n 1 , n 2 ,..., n N . A total Partial molar properties can be calculated from the knowl-
t
property is shown by M where superscript t indicates total edge of relation between M and mole fraction at a given T
(extensive) property and M can be any intensive thermody- and P. One relation that is useful for calculation of ¯ M i is
namic property (i.e., V, H, S, G). In general from the phase the Gibbs–Duhem (GD) equation. This equation is also a use-
rule discussed in Chapter 5 we have
ful relation for obtaining a property of one component in a
mixture from properties of other components. This equation
t
t
(6.75) M = M (T, P, n 1 , n 2 , n 3 , ... , n N ) t
can be derived by total differentiation of M in Eq. (6.75) and
N t
equating with total differential of M from Eq. (6.79), which at
(6.76) n = n i
constant T and P can be reduced to the following simplified
i=1
form [1]:
M t
(6.77) M = (6.81) x i d ¯ M i = 0 (at constant T, P)
n
i
where n is the total number of moles and M is the molar This equation is the constant T and P version of the GD equa-
property of the mixture. Partial molar property of component tion. As an example for a binary system (x 2 = 1 − x 1 ) we can
show that Eqs. (6.80) and (6.81) give the following relations
for calculation of ¯ M i :
45
Lee-Kesler Method for Pentane dM
¯ M 1 = M + x 2
Pentane dx 1
Propane (6.82)
Ethane dM
30 ¯ M 2 = M − x 1
dx 1
C P ig / R - Based on these relations it can be shown that when graphical
presentation of M versus x 1 is available, partial molar proper-
15 ties can be determined from the interceptions of the tangent
line (at x 1 ) with the Y axis. As shown in Fig. 6.4 the intercep-
tion of tangent line at x 1 = 0 gives ¯ M 2 and at x 1 = 1 gives ¯ M 1
according to Eq. (6.82). --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
0
0 500 1000 1500
Example 6.3—Based on the graphical data available on en-
Temperature, K thalpy of aqueous solution of sulfuric acid (H 2 SO 4 ) [1], the
following relation for molar enthalpy of acid solution at 25 C
◦
FIG. 6.3—Prediction of ideal gas heat capacity is obtained:
of some hydrocarbons from Eq. (6.66) and Lee–
3
2
Kesler method (Eq. 6.72). H = 123.7 − 1084.4x w1 + 1004.5x w1 − 1323.2x w1 + 1273.7x 4 w1
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT