Page 269 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: KVU/KXT
QC: —/—
T1: IML
P1: KVU/KXT
20:46
June 22, 2007
AT029-Manual-v7.cls
AT029-06
AT029-Manual
6. THERMODYNAMIC RELATIONS FOR PROPERTY ESTIMATIONS 249
In general the mixtures are divided into two groups of ideal
M 1
solutions and real solutions. An ideal solution is a homoge-
M 2 nous mixture in which all components (like and unlike) have
Molar Property, M solutions have different molecular size and intermolecular
the same molecular size and intermolecular forces, while real
forces. This definition applies to both gas mixtures and liq-
uid mixtures likewise; however, the terms normally are ap-
M
1
plied to liquid solutions. Obviously all ideal gas mixtures are
ideal solutions but not all ideal solutions are ideal gas mix-
M 2
x 1 tures. Mixtures composed of similar components especially
0 0.5 1.0 with similar molecular size and chemical structure are gener-
Mole Fraction, x 1 ally ideal solutions. For example, benzene and toluene form
an ideal solution since both are aromatic hydrocarbons with
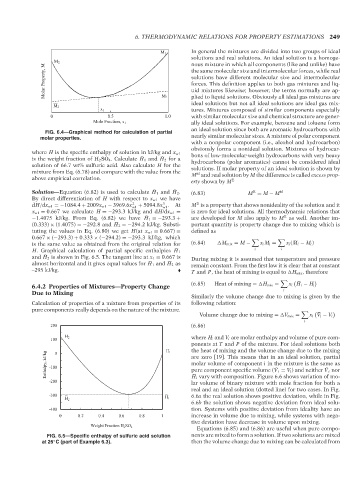
FIG. 6.4—Graphical method for calculation of partial
molar properties. nearly similar molecular sizes. A mixture of polar component
with a nonpolar component (i.e., alcohol and hydrocarbon)
obviously forms a nonideal solution. Mixtures of hydrocar-
where H is the specific enthalpy of solution in kJ/kg and x w1 bons of low-molecular-weight hydrocarbons with very heavy
is the weight fraction of H 2 SO 4 . Calculate ¯ H 1 and ¯ H 2 for a hydrocarbons (polar aromatics) cannot be considered ideal
solution of 66.7 wt% sulfuric acid. Also calculate H for the
mixture from Eq. (6.78) and compare with the value from the solutions. If molar property of an ideal solution is shown by
id
above empirical correlation. M and real solution by M the difference is called excess prop-
E
erty shown by M
Solution—Equation (6.82) is used to calculate ¯ H 1 and ¯ H 2 . (6.83) M = M − M id
E
By direct differentiation of H with respect to x w1 we have
3
E
dH/dx w1 =−1084.4 + 2009x w1 − 3969.6x 2 w1 + 5094.8x . At M is a property that shows nonideality of the solution and it
w1
x w1 = 0.667 we calculate H =−293.3 kJ/kg and dH/dx w1 = is zero for ideal solutions. All thermodynamic relations that
¯ E
−1.4075 kJ/kg. From Eq. (6.82) we have H 1 =−293.3 + are developed for M also apply to M as well. Another im-
(0.333) × (1.4075) =−292.8 and ¯ H 2 =−294.2 kJ/kg. Substi- portant quantity is property change due to mixing which is
tuting the values in Eq. (6.80) we get H(at x w1 = 0.667) = defined as
0.667 × (−293.3) + 0.333 × (−294.2) =−293.3 kJ/kg, which
is the same value as obtained from the original relation for (6.84) M mix = M − x i M i = x i ( ¯ M i − M i )
i i
H. Graphical calculation of partial specific enthalpies ¯ H 1
and ¯ H 2 is shown in Fig. 6.5. The tangent line at x 1 = 0.667 is During mixing it is assumed that temperature and pressure
almost horizontal and it gives equal values for ¯ H 1 and ¯ H 2 as remain constant. From the first law it is clear that at constant
–295 kJ/kg. T and P, the heat of mixing is equal to H mix , therefore
¯
6.4.2 Properties of Mixtures—Property Change (6.85) Heat of mixing = H mix = x i H i − H i
Due to Mixing i
Similarly the volume change due to mixing is given by the
Calculation of properties of a mixture from properties of its following relation:
pure components really depends on the nature of the mixture.

¯
Volume change due to mixing = V mix = x i V i − V i
i
(6.86)
H where H i and V i are molar enthalpy and volume of pure com-
ponents at T and P of the mixture. For ideal solutions both
H the heat of mixing and the volume change due to the mixing
Enthalpy, kJ/kg - molar volume of component i in the mixture is the same as
are zero [19]. This means that in an ideal solution, partial
pure component specific volume ( ¯ V i = V i ) and neither ¯ V i nor
¯ H i vary with composition. Figure 6.6 shows variation of mo-
- lar volume of binary mixture with mole fraction for both a
real and an ideal solution (dotted line) for two cases. In Fig.
- 6.6a the real solution shows positive deviation, while in Fig.
H H
6.6b the solution shows negative deviation from ideal solu-
- tion. Systems with positive deviation from ideality have an
. . . . increase in volume due to mixing, while systems with nega-
tive deviation have decrease in volume upon mixing.
Weight Fraction H SO
Equations (6.85) and (6.86) are useful when pure compo-
FIG. 6.5—Specific enthalpy of sulfuric acid solution nents are mixed to form a solution. If two solutions are mixed
at 25 C (part of Example 6.3). then the volume change due to mixing can be calculated from
◦

--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT