Page 282 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
P2: KVU/KXT
QC: —/—
P1: KVU/KXT
AT029-Manual
AT029-Manual-v7.cls
June 22, 2007
20:46
AT029-06
262 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
where T Mi is the melting point in kelvin and R is the gas con-
f
stant. The ratio H /RT M is dimensionless and represents en- 30 n- Alkylbenzenes
i
tropy of fusion. Unit of H depends on the unit of R. H i f Data
f
i
f
may also be calculated from entropy change of fusion, S ,
i
whenever it is available. 20 Proposed Equation
Won Method
f
(6.158) H = T Mi S i f Entropy of Fusion, ΔS f /.R
i
f
The above equation may also be used to estimate S from
i
f
H calculated through Eq. (6.157). Equation (6.157) can 10
i
reproduce data with average deviations of 12.5, 5.4, and
3.8% for n-alkanes, n-alkylcyclohexanes, and n-alkylbenzens,
respectively. Firoozabadi and co-workers [17, 24–26] have
provided the following equations for calculation of H : 0
f
i
H f 0 5 10 15 20 25 30
i = 0.07177M i for paraffins
RT Mi Carbon Number, NC
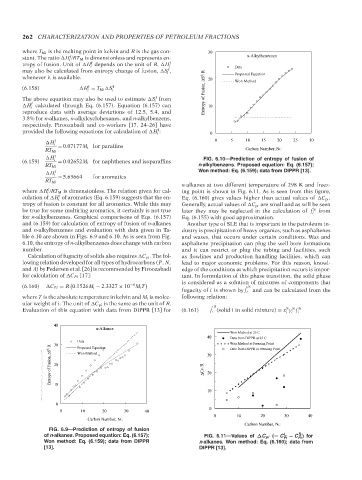
H f FIG. 6.10—Prediction of entropy of fusion of
(6.159) i = 0.02652M i for naphthenes and isoparaffins
RT Mi n-alkylbenzens. Proposed equation: Eq. (6.157);
H f Won method: Eq. (6.159); data from DIPPR [13].
i = 5.63664 for aromatics
RT Mi
n-alkanes at two different temperature of 298 K and freez-
f
where H /RT M is dimensionless. The relation given for cal- ing point is shown in Fig. 6.11. As is seen from this figure,
i
f
culation of H of aromatics (Eq. 6.159) suggests that the en- Eq. (6.160) gives values higher than actual values of C pi .
i
tropy of fusion is constant for all aromatics. While this may Generally, actual values of C pi are small and as will be seen
be true for some multiring aromatics, it certainly is not true later they may be neglected in the calculation of f i S from
for n-alkylbenzenes. Graphical comparisons of Eqs. (6.157) Eq. (6.155) with good approximation.
and (6.159) for calculation of entropy of fusion of n-alkanes Another type of SLE that is important in the petroleum in-
and n-alkylbenzenes and evaluation with data given in Ta- dustry is precipitation of heavy organics, such as asphaltenes
ble 6.10 are shown in Figs. 6.9 and 6.10. As is seen from Fig. and waxes, that occurs under certain conditions. Wax and
6.10, the entropy of n-alkylbenzenes does change with carbon asphaltene precipitation can plug the well bore formations
number. and it can restrict or plug the tubing and facilities, such
Calculation of fugacity of solids also requires C pi . The fol- as flowlines and production handling facilities, which can
lowing relation developed for all types of hydrocarbons (P, N, lead to major economic problems. For this reason, knowl-
and A) by Pedersen et al. [26] is recommended by Firoozabadi edge of the conditions at which precipitation occurs is impor-
for calculation of C Pi [17]: tant. In formulation of this phase transition, the solid phase
is considered as a solution of mixtures of components that
(6.160) C Pi = R 0.1526M i − 2.3327 × 10 −4 M i T S

ˆ
fugacity of i is shown by f i and can be calculated from the
where T is the absolute temperature in kelvin and M i is molec- following relation:
ular weight of i. The unit of C pi is the same as the unit of R. S
ˆ
S
S
Evaluation of this equation with data from DIPPR [13] for (6.161) f i (solid i in solid mixture) = x γ f i S
i
i
40
n-Alkanes
Won Method at 25 C
40 Data from DIPPR at 25 C
Data Won Method at Freezing Point
30
Entropy of Fusion, ΔS f / R 20 Won Method ΔCP /R-- 30
Proposed Equation
Data from DIPPR at Freezing Point
20
10
10
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
0
0
0 10 20 30 40
0 10 20 30 40
Carbon Number, NC
Carbon Number, NC
FIG. 6.9—Prediction of entropy of fusion
L
S
of n-alkanes. Proposed equation: Eq. (6.157); FIG. 6.11—Values of ΔC pi (= C Pi − C )for
Pi
Won method: Eq. (6.159); data from DIPPR n-alkanes. Won method: Eq. (6.160); data from
[13]. DIPPR [13].
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT