Page 284 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: KVU/KXT
QC: —/—
T1: IML
P1: KVU/KXT
20:46
AT029-06
AT029-Manual
June 22, 2007
AT029-Manual-v7.cls
264 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---

Pressure, psia

Enthalpy, Btu/Ib Methane

◦
◦
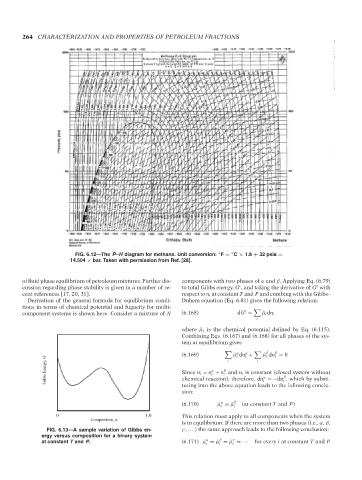
FIG. 6.12—The P–H diagram for methane. Unit conversion: F = C × 1.8 + 32 psia =
14.504 × bar. Taken with permission from Ref. [28].

of fluid phase equilibrium of petroleum mixtures. Further dis- components with two phases of α and β. Applying Eq. (6.79)
cussion regarding phase stability is given in a number of re- to total Gibbs energy, G , and taking the derivative of G with
t
t
cent references [17, 20, 31]. respect to n i at constant T and P and combing with the Gibbs–
Derivation of the general formula for equilibrium condi- Duhem equation (Eq. 6.81) gives the following relation:
tions in terms of chemical potential and fugacity for multi-
t
component systems is shown here. Consider a mixture of N (6.168) dG = ˆ μ i dn i
i
where ˆμ i is the chemical potential defined by Eq. (6.115).
Combining Eqs. (6.167) and (6.168) for all phases of the sys-
tem at equilibrium gives

α α β β
(6.169) i ˆ μ dn + i ˆ μ dn = 0
i
i
i
i
Gibbs Energy, G Since n i = n + n and n i is constant (closed system without
β
α
i
i
β
chemical reaction), therefore, dn =−dn , which by substi-
α
i
i
tuting into the above equation leads to the following conclu-
sion:
(6.170) ˆ μ = ˆμ β (at constant T and P)
α
i i
0 1.0 This relation must apply to all components when the system
Composition, x i
is in equilibrium. If there are more than two phases (i.e., α, β,
FIG. 6.13—A sample variation of Gibbs en- γ , . . . ) the same approach leads to the following conclusion:
ergy versus composition for a binary system
γ
β
α
at constant T and P. (6.171) ˆ μ = ˆμ = ˆμ = ··· for every i at constant T and P
i i i

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT