Page 287 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

T1: IML
QC: —/—
P1: KVU/KXT
P2: KVU/KXT
June 22, 2007
AT029-Manual-v7.cls
AT029-06
AT029-Manual
6. THERMODYNAMIC RELATIONS FOR PROPERTY ESTIMATIONS 267
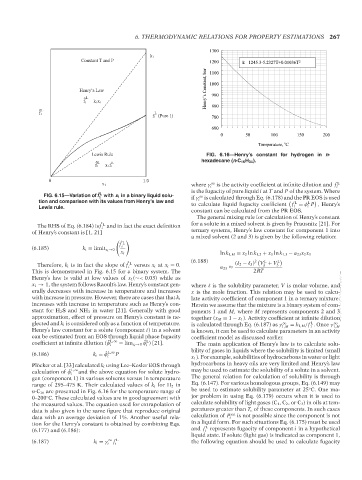
k 1 20:46 1300
Constant T and P 1200 k =1245.3-5.2327T+0.01036T 2
Henry’s Constant, bar 1000
1100
Henry’s Law
^ L 900
f 1 = k 1x 1
800
^ L
f 1 L
f 1 (Pure 1) 700
600
0 50 100 150 200
Temperature, ° C
Lewis Rule FIG. 6.16—Henry’s constant for hydrogen in n-
hexadecane (n-C 16 H 34 ).
^ L L
f 1 = x 1f 1
0 1.0
x 1 where γ i ∞ is the activity coefficient at infinite dilution and f i L
is the fugacity of pure liquid i at T and P of the system. Where
L
FIG. 6.15—Variation of ˆ f with x 1 in a binary liquid solu- if γ ∞ is calculated through Eq. (6.178) and the PR EOS is used
1
i
tion and comparison with its values from Henry’s law and to calculate liquid fugacity coefficient f = φ P , Henry’s
L
L

Lewis rule. i i
constant can be calculated from the PR EOS.
The general mixing rule for calculation of Henry’s constant
The RHS of Eq. (6.184) isf ˆL and in fact the exact definition for a solute in a mixed solvent is given by Prausnitz [21]. For
i
of Henry’s constant is [1, 21] ternary systems, Henry’s law constant for component 1 into
a mixed solvent (2 and 3) is given by the following relation:
ˆL
f
(6.185) k i ≡ limit x i →0 i
x i ln k 1,M = x 2 ln k 1,2 + x 3 ln k 1,3 − α 23 x 2 x 3
(6.188) 2 L L
Therefore, k i is in fact the slope of f ˆL versus x i at x i = 0. α 23 ≈ (δ 2 − δ 3) V + V 3
2
i
This is demonstrated in Fig. 6.15 for a binary system. The 2RT
Henry’s law is valid at low values of x 1 (∼< 0.03) while as
x 1 → 1, the system follows Raoult’s law. Henry’s constant gen- where δ is the solubility parameter, V is molar volume, and
erally decreases with increase in temperature and increases x is the mole fraction. This relation may be used to calcu-
with increase in pressure. However, there are cases that that k i late activity coefficient of component 1 in a ternary mixture. --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
increases with increase in temperature such as Henry’s con- Herein we assume that the mixture is a binary system of com-
stant for H 2 S and NH 3 in water [21]. Generally with good ponents 1 and M, where M represents components 2 and 3
approximation, effect of pressure on Henry’s constant is ne- together (x M = 1 − x 1 ). Activity coefficient at infinite dilution
glected and k i is considered only as a function of temperature. is calculated through Eq. (6.187) as γ 1,M = k 1,M /f . Once γ 1,M
L
∞
∞
1
Henry’s law constant for a solute (component i) in a solvent is known, it can be used to calculate parameters in an activity
can be estimated from an EOS through liquid phase fugacity coefficient model as discussed earlier.
ˆ L
coefficient at infinite dilution ( ˆ φ L,∞ = lim x i →0 φ ) [21].
i i The main application of Henry’s law is to calculate solu-
bility of gases in liquids where the solubility is limited (small
(6.186) k i = ˆ φ L,∞ P
i x 1 ). For example, solubilities of hydrocarbons in water or light
Pl¨ocker et al. [33] calculated k i using Lee–Kesler EOS through hydrocarbons in heavy oils are very limited and Henry’s law
calculation of ˆ φ i L,∞ and the above equation for solute hydro- may be used to estimate the solubility of a solute in a solvent.
gen (component 1) in various solvents versus in temperature The general relation for calculation of solubility is through
range of 295–475 K. Their calculated values of k i for H 2 in Eq. (6.147). For various homologous groups, Eq. (6.149) may
◦
n-C 16 are presented in Fig. 6.16 for the temperature range of be used to estimate solubility parameter at 25 C. One ma-
0–200 C. These calculated values are in good agreement with jor problem in using Eq. (6.179) occurs when it is used to
◦
the measured values. The equation used for extrapolation of calculate solubility of light gases (C 1 ,C 2 ,orC 3 ) in oils at tem-
data is also given in the same figure that reproduce original peratures greater than T c of these components. In such cases
sat
data with an average deviation of 1%. Another useful rela- calculation of P i is not possible since the component is not
tion for the Henry’s constant is obtained by combining Eqs. in a liquid form. For such situations Eq. (6.175) must be used
L
(6.177) and (6.186): and f represents fugacity of component i in a hypothetical
i
liquid state. If solute (light gas) is indicated as component 1,
(6.187) k i = γ ∞ f L the following equation should be used to calculate fugacity
i i

Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT