Page 324 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

P2: IML/FFX
QC: IML/FFX
T1: IML
P1: IML/FFX
AT029-07
AT029-Manual-v7.cls
17:40
June 22, 2007
304 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
L
3
S
3
S
Formula
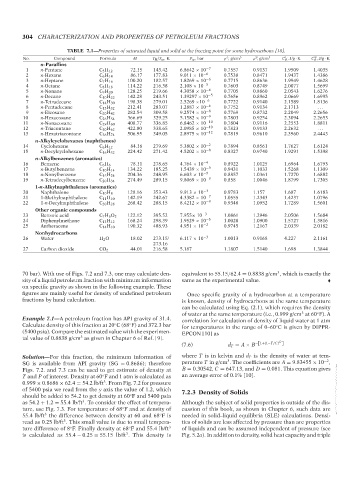
No. AT029-Manual TABLE 7.1—Properties of saturated liquid and solid at the freezing point for some hydrocarbons [10]. P L C , J/g · K
Compound
ρ , g/cm
ρ , g/cm
C , J/g · K
M
T M /T tp ,K
P tp ,bar
P
n-Paraffins
1 n-Pentane C 5 H 12 72.15 143.42 6.8642 × 10 −7 0.7557 0.9137 1.9509 1.4035
2 n-Hexane C 6 H 14 86.17 177.83 9.011 × 10 −6 0.7538 0.8471 1.9437 1.4386
3 n-Heptane C 7 H 16 100.20 182.57 1.8269 × 10 −6 0.7715 0.8636 1.9949 1.4628
4 n-Octane C 8 H 18 114.22 216.38 2.108 × 10 −5 0.7603 0.8749 2.0077 1.5699
5 n-Nonane C 9 H 20 128.25 219.66 4.3058 × 10 −6 0.7705 0.8860 2.0543 1.6276
6 n-Decane C 10 H 22 142.28 243.51 1.39297 × 10 −5 0.7656 0.8962 2.0669 1.6995
7 n-Tetradecane C 14 H 30 198.38 279.01 2.5269 ×10 −6 0.7722 0.9140 2.1589 1.8136
8 n-Pentadecane C 15 H 32 212.41 283.07 1.2887 × 10 −6 0.7752 0.9134 2.1713 . . .
9 n-Eicosane C 20 H 42 282.54 309.58 9.2574 × 10 −8 0.7769 0.8732 2.2049 2.2656
10 n-Hexacosane C 26 H 54 366.69 329.25 5.1582 × 10 −9 0.7803 0.9254 2.3094 2.2653
11 n-Nonacosane C 29 H 60 408.77 336.85 6.8462 × 10 −10 0.7804 0.9116 2.2553 1.8811
12 n-Triacontane C 30 H 62 422.80 338.65 2.0985 × 10 −10 0.7823 0.9133 2.2632 . . .
13 n-Hexatriacontane C 36 H 74 506.95 349.05 2.8975 × 10 −12 0.7819 0.9610 2.3960 2.4443
n-Alkylcyclohexanes (naphthenes)
14 Cyclohexane C 6 H 12 84.16 279.69 5.3802 × 10 −2 0.7894 0.8561 1.7627 1.6124
15 n-Decylcyclohexane C 16 H 32 224.42 271.42 4.5202 × 10 −8 0.8327 0.9740 1.9291 1.5398
n-Alkylbenzenes (aromatics)
16 Benzene C 6 H 6 78.11 278.65 4.764 × 10 −4 0.8922 1.0125 1.6964 1.6793
17 n-Butylbenzene C 10 H 14 134.22 185.25 1.5439 × 10 −9 0.9431 1.1033 1.5268 1.1309
18 n-Nonylbenzene C 15 H 24 204.36 248.95 6.603 × 10 −9 0.8857 1.0361 1.7270 1.6882
19 n-Tetradecylbenzene C 20 H 34 274.49 289.15 9.8069 × 10 −9 0.858 1.0046 1.8799 1.7305
1-n-Alkylnaphthalenes (aromatics)
20 Naphthalene C 10 H 8 128.16 353.43 9.913 × 10 −3 0.9783 1.157 1.687 1.6183
21 1-Methylnaphthalene C 11 H 10 142.19 242.67 4.3382 × 10 −7 1.0555 1.2343 1.4237 1.0796
22 1-n-Decylnaphthalene C 20 H 28 268.42 288.15 8.4212 × 10 −9 0.9348 1.0952 1.7289 1.5601
Other organic compounds
23 Benzoic acid C 7 H 6 O 2 122.12 395.52 7.955× 10 −3 1.0861 1.2946 2.0506 1.5684
24 Diphenylmethane C 13 H 12 168.24 298.39 1.9529 × 10 −5 1.0020 1.0900 1.5727 1.3816
25 Antheracene C 14 H 10 190.32 488.93 4.951 × 10 −2 0.9745 1.2167 2.0339 2.0182
Nonhydrocarbons
26 Water H 2 O 18.02 273.15/ 6.117 × 10 −3 1.0013 0.9168 4.227 2.1161
273.16
27 Carbon dioxide CO 2 44.01 216.58 5.187 1.1807 1.5140 1.698 1.3844
3
70 bar). With use of Figs. 7.2 and 7.3, one may calculate den- equivalent to 55.15/62.4 = 0.8838 g/cm , which is exactly the
sity of a liquid petroleum fraction with minimum information same as the experimental value.
on specific gravity as shown in the following example. These
figures are mainly useful for density of undefined petroleum Once specific gravity of a hydrocarbon at a temperature
fractions by hand calculation. is known, density of hydrocarbons at the same temperature
can be calculated using Eq. (2.1), which requires the density
3
of water at the same temperature (i.e., 0.999 g/cm at 60 F). A
◦
Example 7.1—A petroleum fraction has API gravity of 31.4. correlation for calculation of density of liquid water at 1 atm
Calculate density of this fraction at 20 C (68 F) and 372.3 bar for temperatures in the range of 0–60 C is given by DIPPR-
◦
◦
◦
(5400 psia). Compare the estimated value with the experimen- EPCON [10] as
3
tal value of 0.8838 g/cm as given in Chapter 6 of Ref. [9].
D
(7.6) d T = A × B −[ 1+(1−T/C) ]
Solution—For this fraction, the minimum information of where T is in kelvin and d T is the density of water at tem-
3
−2
SG is available from API gravity (SG = 0.8686); therefore perature T in g/cm . The coefficients are A = 9.83455 × 10 ,
Figs. 7.2. and 7.3 can be used to get estimate of density at B = 0.30542, C = 647.13, and D = 0.081. This equation gives
T and P of interest. Density at 60 F and 1 atm is calculated as an average error of 0.1% [10].
◦
3
0.999 × 0.8686 × 62.4 = 54.2 lb/ft . From Fig. 7.2 for pressure
of 5400 psia we read from the y axis the value of 1.2, which 7.2.3 Density of Solids --`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
should be added to 54.2 to get density at 60 F and 5400 psia
◦
3
as 54.2 + 1.2 = 55.4 lb/ft . To consider the effect of tempera- Although the subject of solid properties is outside of the dis-
ture, use Fig. 7.3. For temperature of 68 F and at density of cussion of this book, as shown in Chapter 6, such data are
◦
3
55.4 lb/ft the difference between density at 60 and 68 Fis needed in solid–liquid equilibria (SLE) calculations. Densi-
◦
3
read as 0.25 lb/ft . This small value is due to small tempera- ties of solids are less affected by pressure than are properties
ture difference of 8 F. Finally density at 68 F and 55.4 lb/ft 3 of liquids and can be assumed independent of pressure (see
◦
◦
3
is calculated as 55.4 − 0.25 = 55.15 lb/ft . This density is Fig. 5.2a). In addition to density, solid heat capacity and triple
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT