Page 326 - Characterization and Properties of Petroleum Fractions - M.R. Riazi

QC: IML/FFX
P2: IML/FFX
P1: IML/FFX
June 22, 2007
AT029-Manual
AT029-07
306 CHARACTERIZATION AND PROPERTIES OF PETROLEUM FRACTIONS
1000
100 AT029-Manual-v7.cls T1: IML 17:40

10

1

TECHNICAL DATA BOOK
February 1994
0.1
–50 –25 0 25 50 75 100 150 200 250 300 400 500

◦ ◦
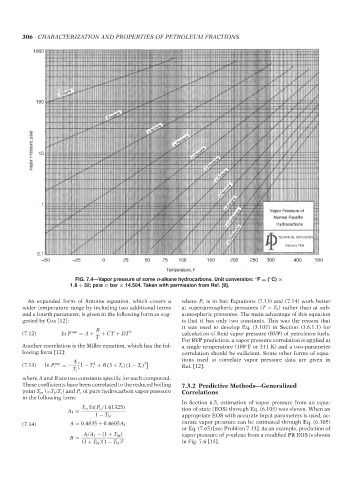
FIG. 7.4—Vapor pressure of some n-alkane hydrocarbons. Unit conversion: F = ( C) ×
1.8 + 32; psia = bar × 14.504. Taken with permission from Ref. [9].

An expanded form of Antoine equation, which covers a where P c is in bar. Equations (7.13) and (7.14) work better
wider temperature range by including two additional terms at superatmospheric pressures (T > T b ) rather than at sub-
and a fourth parameter, is given in the following form as sug- atmospheric pressures. The main advantage of this equation
gested by Cox [12]: is that it has only two constants. This was the reason that
it was used to develop Eq. (3.102) in Section (3.6.1.1) for
B
(7.12) ln P vap = A + + CT + DT 2 calculation of Reid vapor pressure (RVP) of petroleum fuels.
T
For RVP prediction, a vapor pressure correlation is applied at
Another correlation is the Miller equation, which has the fol- a single temperature (100 F or 311 K) and a two-parameter
◦
lowing form [12]: correlation should be sufficient. Some other forms of equa-
tions used to correlate vapor pressure data are given in
2
(7.13) ln P r vap =− A 1 − T + B (3 + T r)(1 − T r) 3 Ref. [12].
r
T r
where A and B are two constants specific for each compound.
These coefficients have been correlated to the reduced boiling 7.3.2 Predictive Methods—Generalized
point T br (=T b /T c ) and P c of pure hydrocarbon vapor pressure Correlations
in the following form:
In Section 6.5, estimation of vapor pressure from an equa-
T br ln(P c /1.01325) tion of state (EOS) through Eq. (6.105) was shown. When an
A 1 =
1 − T br appropriate EOS with accurate input parameters is used, ac-
(7.14) A = 0.4835 + 0.4605A 1 curate vapor pressure can be estimated through Eq. (6.105)
or Eq. (7.65) [see Problem 7.13]. As an example, prediction of
A/A 1 − (1 + T br ) vapor pressure of p-xylene from a modified PR EOS is shown
B =
(3 + T br )(1 − T br ) 2 in Fig. 7.6 [14].

--`,```,`,``````,`,````,```,,-`-`,,`,,`,`,,`---
Copyright ASTM International
Provided by IHS Markit under license with ASTM Licensee=International Dealers Demo/2222333001, User=Anggiansah, Erick
No reproduction or networking permitted without license from IHS Not for Resale, 08/26/2021 21:56:35 MDT