Page 418 - Mechanical Behavior of Materials

Section 9.2 Definitions and Concepts 419

σ σ max σ σ max
σ a σ m σ a
0 Δσ time Δσ
σ a 0 σ a
σ min σ
one cycle min
(a) (b)

σ max = Δσ
σ
σ a
(c)
σ a
0

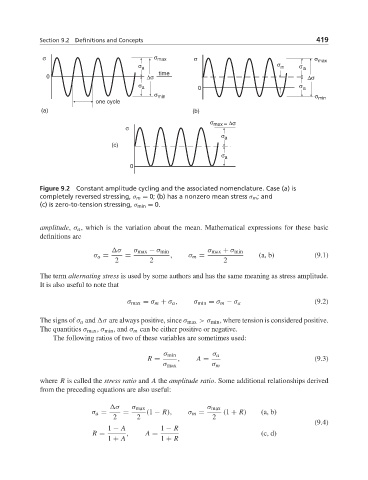
Figure 9.2 Constant amplitude cycling and the associated nomenclature. Case (a) is
completely reversed stressing, σ m = 0; (b) has a nonzero mean stress σ m ;and
(c) is zero-to-tension stressing, σ min = 0.

amplitude, σ a , which is the variation about the mean. Mathematical expressions for these basic
definitions are
σ σ max − σ min σ max + σ min
σ a = = , σ m = (a, b) (9.1)
2 2 2

The term alternating stress is used by some authors and has the same meaning as stress amplitude.
It is also useful to note that

σ max = σ m + σ a , σ min = σ m − σ a (9.2)

The signs of σ a and σ are always positive, since σ max >σ min , where tension is considered positive.
The quantities σ max , σ min , and σ m can be either positive or negative.
The following ratios of two of these variables are sometimes used:

σ min σ a
R = , A = (9.3)
σ max σ m
where R is called the stress ratio and A the amplitude ratio. Some additional relationships derived
from the preceding equations are also useful:

σ σ max σ max
σ a = = (1 − R), σ m = (1 + R) (a, b)
2 2 2
(9.4)
1 − A 1 − R
R = , A = (c, d)
1 + A 1 + R