Page 63 - Petroleum Production Engineering, A Computer-Assisted Approach

Guo, Boyun / Petroleum Production Engineering, A Computer-Assisted Approach 0750682701_chap04 Final Proof page 54 22.12.2006 6:07pm

4/54 PETROLEUM PRODUCTION ENGINEERING FUNDAMENTALS
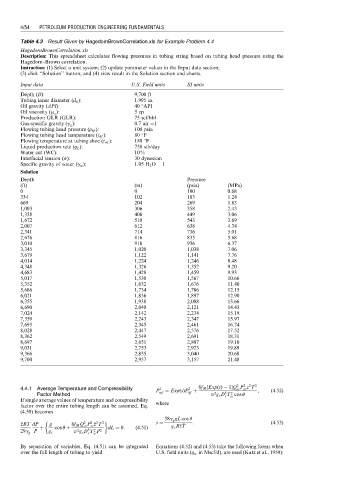
Table 4.3 Result Given by HagedornBrownCorrelation.xls for Example Problem 4.4
HagedornBrownCorrelation.xls
Description: This spreadsheet calculates flowing pressures in tubing string based on tubing head pressure using the
Hagedorn–Brown correlation.
Instruction: (1) Select a unit system; (2) update parameter values in the Input data section;
(3) click ‘‘Solution’’ button; and (4) view result in the Solution section and charts.
Input data U.S. Field units SI units
Depth (D): 9,700 ft
Tubing inner diameter (d ti ): 1.995 in.
Oil gravity (API): 40 8API
Oil viscosity (m o ): 5 cp
Production GLR (GLR): 75 scf/bbl
Gas-specific gravity (g g ): 0.7 air ¼1
Flowing tubing head pressure (p hf ): 100 psia
Flowing tubing head temperature (t hf ): 80 8F
Flowing temperature at tubing shoe (t wf ): 180 8F
Liquid production rate (q L ): 758 stb/day
Water cut (WC): 10 %
Interfacial tension (s): 30 dynes/cm
Specific gravity of water (g w ): 1.05 H 2 O ¼ 1
Solution
Depth Pressure
(ft) (m) (psia) (MPa)
0 0 100 0.68
334 102 183 1.24
669 204 269 1.83
1,003 306 358 2.43
1,338 408 449 3.06
1,672 510 543 3.69
2,007 612 638 4.34
2,341 714 736 5.01
2,676 816 835 5.68
3,010 918 936 6.37
3,345 1,020 1,038 7.06
3,679 1,122 1,141 7.76
4,014 1,224 1,246 8.48
4,348 1,326 1,352 9.20
4,683 1,428 1,459 9.93
5,017 1,530 1,567 10.66
5,352 1,632 1,676 11.40
5,686 1,734 1,786 12.15
6,021 1,836 1,897 12.90
6,355 1,938 2,008 13.66
6,690 2,040 2,121 14.43
7,024 2,142 2,234 15.19
7,359 2,243 2,347 15.97
7,693 2,345 2,461 16.74
8,028 2,447 2,576 17.52
8,362 2,549 2,691 18.31
8,697 2,651 2,807 19.10
9,031 2,753 2,923 19.89
9,366 2,855 3,040 20.68
9,700 2,957 3,157 21.48

2
2
2
z
T
z
4.4.1 Average Temperature and Compressibility P 2 ¼ Exp(s)P þ 8f M [Exp(s) 1]Q P T 2 , (4:52)
sc
sc
2
5
2
2
Factor Method wf hf p g c D T cos u
sc
i
If single average values of temperature and compressibility
factor over the entire tubing length can be assumed, Eq. where
(4.50) becomes
58g g gL cos u
2
2
2
z
T
zzR T dP g 8f M Q P z T 2 s ¼ : (4:53)
T
T
zT
þ cos u þ cs sc dL ¼ 0: (4:51) g c R z
5
2
29g g P g c p g c D T P 2
2
sc
i
By separation of variables, Eq. (4.51) can be integrated Equations (4.52) and (4.53) take the following forms when
over the full length of tubing to yield U.S. field units (q sc in Mscf/d), are used (Katz et al., 1959):